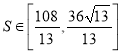题目内容
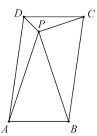
【题目】如图所示,已知焦点为![]() 的抛物线
的抛物线![]() 上有一动点
上有一动点![]() ,过点
,过点![]() 作抛物线的切线
作抛物线的切线![]() 交
交![]() 轴于点
轴于点![]() .
.
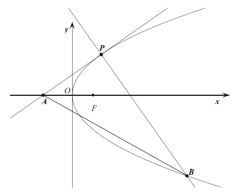
(1)判断线段![]() 的中垂线是否过定点,若是求出定点坐标,若不是说明理由;
的中垂线是否过定点,若是求出定点坐标,若不是说明理由;
(2)过点![]() 作
作![]() 的垂线交抛物线于另一点
的垂线交抛物线于另一点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(1)存在,过定点![]() ;(2)
;(2)![]() .
.
【解析】
(1)设直线![]() 的方程为
的方程为![]() 与抛物线方程联立方程组,消元后由判别式为0得
与抛物线方程联立方程组,消元后由判别式为0得![]() ,这样可用
,这样可用![]() 表示出
表示出![]() 点坐标,从而也可得
点坐标,从而也可得![]() 点坐标,然后求出
点坐标,然后求出![]() 中垂线方程后可得定点;
中垂线方程后可得定点;
(2)在(1)基础上,求出![]() 方程,与抛物线方程联立求得
方程,与抛物线方程联立求得![]() 点坐标后,计算出
点坐标后,计算出![]() ,
,![]() ,从而得
,从而得![]() 面积
面积![]() 为
为![]() 的函数,其中
的函数,其中![]() ,利用导数可求得其最小值.
,利用导数可求得其最小值.
(1)设直线![]() 的方程为
的方程为![]() 和抛物线方程
和抛物线方程![]() 联立得:
联立得:![]() ,
,
由![]() ,
,![]() 得
得![]() ,则
,则![]() 的解为
的解为![]() ,由
,由![]() 得
得![]() ,
,![]() ,得
,得![]() ,在
,在![]() 中令
中令![]() 得
得![]() ,所以
,所以![]() ,
,
![]() 中点为
中点为![]() ,所以线段
,所以线段![]() 的中垂线方程为
的中垂线方程为![]() ,
,
所以线段![]() 的中垂线过定点
的中垂线过定点![]() .
.
(2)直线![]() 的方程为
的方程为![]() 和抛物线方程
和抛物线方程![]() 联立得:
联立得:
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以![]() 的面积为
的面积为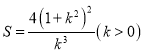 ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以![]() 时,
时,![]() .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目