题目内容
【题目】已知以点![]() 为圆心的圆经过点
为圆心的圆经过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() 和
和![]() ,且
,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)求圆![]() 的方程;
的方程;
(3)设点![]() 在圆
在圆![]() 上,试问使△
上,试问使△![]() 的面积等于8的点
的面积等于8的点![]() 共有几个?证明你的结论.
共有几个?证明你的结论.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)两个.
;(3)两个.
【解析】
试题分析:(1)求出![]() 中点坐标,且
中点坐标,且![]() 的斜率与
的斜率与![]() 的斜率互为负倒数,可得
的斜率互为负倒数,可得![]() 方程;(2)要求圆的方程,关键是求出圆心坐标,(半径已知是
方程;(2)要求圆的方程,关键是求出圆心坐标,(半径已知是![]() ),可设圆心为
),可设圆心为![]() ,由圆心在直线
,由圆心在直线![]() 上,且半径为
上,且半径为![]() 联立方程组可解得;(3)由三角形面积为8,可得
联立方程组可解得;(3)由三角形面积为8,可得![]() 边上的高为
边上的高为![]() ,即
,即![]() 到
到![]() 的距离,下面只要判断圆上有几个点到直线
的距离,下面只要判断圆上有几个点到直线![]() 的距离为
的距离为![]() ,也即判断到直线
,也即判断到直线![]() 距离为
距离为![]() 的两条平行线与圆的位置关系.
的两条平行线与圆的位置关系.
试题解析:⑴直线![]() 的斜率
的斜率![]() ,
,![]() 中点坐标为
中点坐标为![]() ,
,
∴直线![]() 方程为
方程为![]()
⑵设圆心![]() ,则由
,则由![]() 在
在![]() 上得:
上得:![]() ①
①
又直径![]() ,
,![]() ,
, ![]() ②
②
由①②解得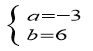 或
或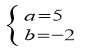
∴圆心![]() 或
或![]() .
.
∴圆![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)![]() ,
,
∴当![]() 面积为8时,点
面积为8时,点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
又圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,圆
,圆![]() 的半径
的半径![]() ,且
,且![]() ,
,
∴圆上共有两个点![]() 使
使![]() 面积为8.
面积为8.

练习册系列答案
相关题目


