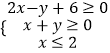题目内容
【题目】已知圆![]() 、圆
、圆![]() 均满足圆心在直线
均满足圆心在直线![]() :
: ![]() 上,过点
上,过点![]() ,且与直线l2:x=-1相切.
,且与直线l2:x=-1相切.
(1)当![]() 时,求圆
时,求圆![]() ,圆
,圆![]() 的标准方程;
的标准方程;
(2)直线l2与圆![]() 、圆
、圆![]() 分别相切于A,B两点,求
分别相切于A,B两点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)设出圆的标准方程,圆心为(an,bn),半径为rm,根据已知条件列方程,解方程即可;
(2)根据圆过(1,0),与x=-1相切,且圆心在直线x-my-2=0上,得方程b2-4mb-8=0,结合图象,用含m的式子表示出![]() ,进而求出
,进而求出![]() 的最小值。
的最小值。
设圆![]() .
.
依题意得: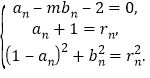
消去![]() 得
得
消去![]() 得
得![]() .
.
(1)当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以圆![]() ,圆
,圆![]() 的标准方程分别为:
的标准方程分别为:![]() ,
,![]() .
.
(2)根据题意,如图:
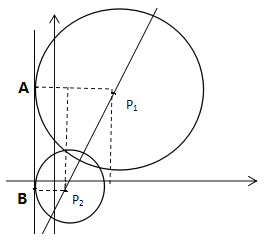
设圆的方程为(x-a)2+(y-b)2=r2,
已知过(1,0),得方程(1-a)2+b2=r2 ① ![]()
已知圆心在直线![]()
![]() 上 ,得方程a-mb-2=0,得a=mb+2 ②,
上 ,得方程a-mb-2=0,得a=mb+2 ②,
已知直线l :x=-1与圆切与A,B,得r=a+1 ③
综合①②③得b2-4mb-8=0,
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.
故当且仅当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.

练习册系列答案
相关题目
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0. 05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.