题目内容
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,长轴端点为
,长轴端点为![]() ,
,![]() ,
,![]() 为椭圆中心,
为椭圆中心,![]() ,斜率为
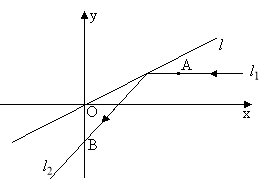
,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点,这两点在
交于不同的两点,这两点在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的两个焦点.
的两个焦点.

(1)求椭圆![]() 的方程;
的方程;
(2)若抛物线![]() 上存在两个点
上存在两个点![]() ,
,![]() ,椭圆
,椭圆![]() 上存在两个点
上存在两个点![]() ,
,![]() ,满足
,满足![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,
,![]() ,
,![]() 三点共线,且
三点共线,且![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由![]() ,可得
,可得![]() ,由于斜率为
,由于斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点,这两点在
交于不同的两点,这两点在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的两个焦点,可知直线过原点,表示出直线方程,可得直线与椭圆的一个交点坐标,代入椭圆中,可得到
的两个焦点,可知直线过原点,表示出直线方程,可得直线与椭圆的一个交点坐标,代入椭圆中,可得到![]() ,
,![]() 的值,由此得到椭圆的方程。
的值,由此得到椭圆的方程。
(2)分类讨论直线![]() 斜率存在与不存在的情况,当斜率不存在时,根据题意可得
斜率存在与不存在的情况,当斜率不存在时,根据题意可得![]() ,
,![]() ,即可得到四边形
,即可得到四边形![]() 的面积,当斜率
的面积,当斜率![]() 存在时,设出直线
存在时,设出直线![]() 的点斜式方程以及直线
的点斜式方程以及直线![]() 的方程,将直线
的方程,将直线![]() 的方程与抛物线联立方程,得到关于
的方程与抛物线联立方程,得到关于![]() 的一元二次方程,由弦长公式表示出
的一元二次方程,由弦长公式表示出![]() ,再联立直线
,再联立直线![]() 与椭圆的方程,得出
与椭圆的方程,得出![]() 的长,最后表示出四边形
的长,最后表示出四边形![]() 面积关于斜率
面积关于斜率![]() 的表达式,利用基本不等式即可求出四边形
的表达式,利用基本不等式即可求出四边形![]() 面积最小值。
面积最小值。
解:(1)设椭圆方程为![]() ,
,
利用数量积运算可得![]() ,可得
,可得![]() ,
,
直线![]() 的方程为
的方程为![]() ,当
,当![]() 时,
时,![]() ,
,
代入椭圆方程可得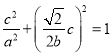 ,
,
联立解得![]() ,
,![]() ,椭圆方程
,椭圆方程![]() .
.
(2)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的斜率为0,得到
的斜率为0,得到![]() ,
,![]() ,
,![]() ;
;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程为
方程为![]() ,
,
与抛物线![]() 联立得
联立得![]() 。
。
令![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
因为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
将直线![]() 与椭圆联立,得
与椭圆联立,得![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,
所以四边形![]() 面积
面积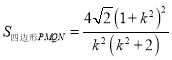 ,
,
令![]() ,
,
则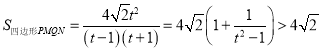 ,
,
所以![]() ,其最小值为
,其最小值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】![]() 是指悬浮在空气中的空气动力学当量直径小于或等于
是指悬浮在空气中的空气动力学当量直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准
微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准![]() ,
,![]() 日均值在
日均值在![]() 微克/立方米以下,空气质量为一级;在
微克/立方米以下,空气质量为一级;在![]() 微克应立方米
微克应立方米![]() 微克立方米之间,空气质量为二级:在
微克立方米之间,空气质量为二级:在![]() 微克/立方米以上,空气质量为超标.从某市
微克/立方米以上,空气质量为超标.从某市![]() 年全年每天的
年全年每天的![]() 监测数据中随机地抽取
监测数据中随机地抽取![]() 天的数据作为样本,监测值频数如下表:
天的数据作为样本,监测值频数如下表:
(微克/立方米) |
|
|
|
|
|
|
频数(天) |
|
|
|
|
|
|
(1)从这![]() 天的
天的![]() 日均值监测数据中,随机抽出
日均值监测数据中,随机抽出![]() 天,求恰有
天,求恰有![]() 天空气质量达到一级的概率;
天空气质量达到一级的概率;
(2)从这![]() 天的数据中任取
天的数据中任取![]() 天数据,记
天数据,记![]() 表示抽到
表示抽到![]() 监测数据超标的天数,求
监测数据超标的天数,求![]() 的分布列.
的分布列.
【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率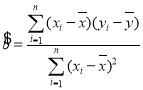 ;相关系数
;相关系数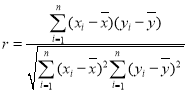 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |