题目内容
双曲线
-
=1左右焦点分别为F1,F2,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|等于( )
| x2 |
| 8 |
| y2 |
| 4 |
A.2
| B.4
| C.8
| D.8 |
由题意可知 2b=4,e=
=
,于是 a=2
,
∵2|AB|=|AF2|+|BF2|,
∴|AB|+|AF1|+|BF1|=|AF2|+|BF2|,
得|AB|=|AF2|-|AF1|+|BF2|-|BF1|=4a=8
.
故选C.
| c |
| a |
| ||
| 2 |
| 2 |
∵2|AB|=|AF2|+|BF2|,
∴|AB|+|AF1|+|BF1|=|AF2|+|BF2|,
得|AB|=|AF2|-|AF1|+|BF2|-|BF1|=4a=8
| 2 |
故选C.

练习册系列答案
相关题目
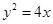 的焦点坐标为 .
的焦点坐标为 .