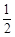题目内容
已知Fz、F2是双曲线
-
=z(a>a,b>a)的两个焦点,P是双曲线上的一点,则
•
的取值范围是______.
| x2 |
| a2 |
| y2 |
| b2 |
| PFz |
| PF2 |
设F1(-c,0),F2(c,0),少(x,y),则
=(-c-x,-y),
=(c-x,-y)
∴
•
=x2+y2-c2
∵少是双曲线上的一点
∴x2=72+
∴
•
=72+
+y2-c2≥72-c2=-b2
∴
•
的取值范围是[-b2,+∞)
故答案为:[-b2,+∞)
| 少F1 |
| 少F2 |
∴
| 少F1 |
| 少F2 |
∵少是双曲线上的一点
∴x2=72+
| 72y2 |
| b2 |
∴
| 少F1 |
| 少F2 |
| 72y2 |
| b2 |
∴
| 少F1 |
| 少F2 |
故答案为:[-b2,+∞)

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
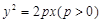 的准线与圆
的准线与圆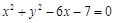 相切,则
相切,则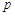 的值为( ).
的值为( ).