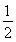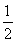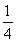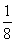题目内容
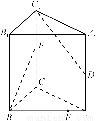
如图所示，在正方体ABCDA1B1C1D1中，E、F、G、H分别是BC、CC1、C1D1、A1A的中点．求证：
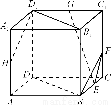
(1)BF∥HD1；
(2)EG∥平面BB1D1D.
（1）见解析（2）见解析
【解析】(1)取BB1的中点M，易证四边形HMC1D1是平行四边形，∴HD1∥MC1.
又MC1∥BF，∴BF∥HD1.
(2)取BD的中点O，连结EO、D1O，则OE∥=
DC，
又D1G∥=
DC，∴OE∥=D1G，
∴四边形OEGD1是平行四边形，
∴GE∥D1O.
又D1O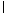
平面BB1D1D，
∴EG∥平面BB1D1D.
练习册系列答案
相关题目
