题目内容
已知对任意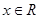 ,
, 恒成立(其中
恒成立(其中 ),求
),求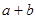 的最大值.
的最大值.
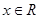 ,
, 恒成立(其中
恒成立(其中 ),求
),求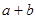 的最大值.
的最大值.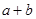 的最大值为
的最大值为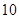 .
.试题分析:利用二倍角公式
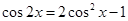 ,利用换元法
,利用换元法 ,将原不等式转化为二次不等式
,将原不等式转化为二次不等式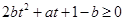 在区间
在区间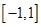 上恒成立,利用二次函数的零点分布进行讨论,从而得出
上恒成立,利用二次函数的零点分布进行讨论,从而得出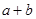 的最大值,但是在对
的最大值,但是在对 时的情况下,主要对二次函数的对称轴
时的情况下,主要对二次函数的对称轴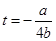 是否在区间
是否在区间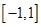 进行分类讨论,再将问题转化为
进行分类讨论,再将问题转化为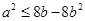 的条件下,求
的条件下,求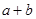 的最大值,
的最大值,试题解析:由题意知
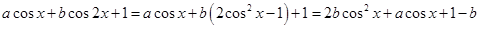 ,
,令
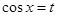 ,
,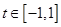 ,则当
,则当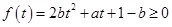 ,
,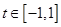 恒成立,开口向上,
恒成立,开口向上,①当
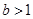 时,
时,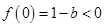 ,不满足
,不满足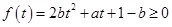 ,
,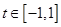 恒成立,
恒成立,②当
 时,则必有
时,则必有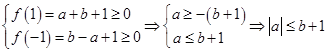 (1)
(1)当对称轴
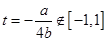 时,即
时,即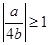 ,也即
,也即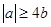 时,有
时,有 ,
,则
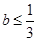 ,
,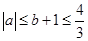 ,则
,则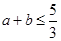 ,当
,当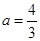 ,
,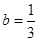 时,
时,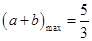 .
.当对称轴
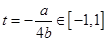 时,即
时,即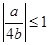 ,也即
,也即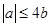 时,
时,则必有
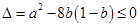 ,即
,即 ,又由(1)知
,又由(1)知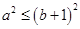 ,
,则由于
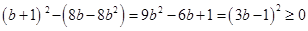 ,故只需
,故只需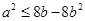 成立即可,
成立即可,问题转化为
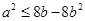 的条件下,求
的条件下,求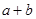 的最大值,然后利用代数式的结构特点或从题干中的式子出发,分别利用三角换元法、导数法以及柯西不等式法来求
的最大值,然后利用代数式的结构特点或从题干中的式子出发,分别利用三角换元法、导数法以及柯西不等式法来求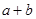 的最大值.
的最大值.法一:(三角换元)把条件配方得:
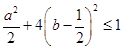 ,
,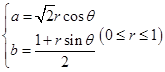 ,所以
,所以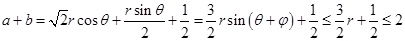 ,
,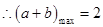 ;
;法二:(导数)
令
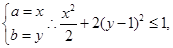 则即求函数的导数,椭圆的上半部分
则即求函数的导数,椭圆的上半部分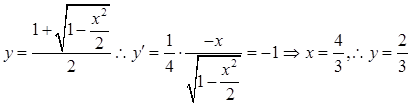
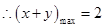 ;
;法三:(柯西不等式)由柯西不等式可知:
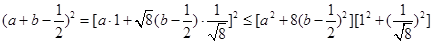
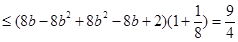 ,当且仅当
,当且仅当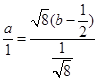 ,即
,即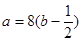 及
及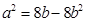 时等号成立.即当
时等号成立.即当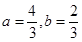 时,
时,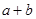 最大值为2.
最大值为2.综上可知
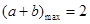 .
.
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
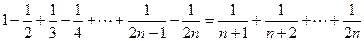
 ,
, ,
, ,且
,且 .求证:
.求证: .
.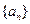 中,
中,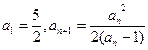
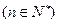 ,用数学归纳法证明:
,用数学归纳法证明: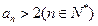
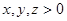 ,则
,则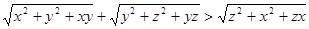
 >
> ,x>y. 求证:
,x>y. 求证: >
> .
. ,则函数
,则函数 的最大值为( )
的最大值为( )


