题目内容
【题目】在某次会操活动中,领操员让编号为![]() 的
的![]() 名学生排成一个圆形阵,做
名学生排成一个圆形阵,做![]() 循环报数,领操员一一记录报数者的编号,并要求报l、2的学生出列,报3的学生留在队列中,并将编号改为此次循环报数中三名学生的编号之和.一直循环报数下去.当操场上剩余的学生人数不超过两名时,报数活动结束.领操员记录最后留在操场的学生编号(例如,编号为
循环报数,领操员一一记录报数者的编号,并要求报l、2的学生出列,报3的学生留在队列中,并将编号改为此次循环报数中三名学生的编号之和.一直循环报数下去.当操场上剩余的学生人数不超过两名时,报数活动结束.领操员记录最后留在操场的学生编号(例如,编号为![]() 的九名学生排成一个圆形阵,报数结束后,只有原始编号为9的学生留在操场,此时,他的编号为45,领操员记录下来的数据分别为l,2,3,4,5,6,7,8,9,6,15,24,45).已知共有2011名学生参加会操.
的九名学生排成一个圆形阵,报数结束后,只有原始编号为9的学生留在操场,此时,他的编号为45,领操员记录下来的数据分别为l,2,3,4,5,6,7,8,9,6,15,24,45).已知共有2011名学生参加会操.
(1)最后留在场内的学生最初的编号是几号?
(2)求领操员记录下的编号之和.
【答案】(1)1923;(2)![]()
【解析】
记领操员记录下的编号依次为![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,
,…,![]() ,其和为
,其和为![]() .于是,
.于是,
(1)在每次![]() 循环报数后,学生总人数减少2,但编号之和不变.
循环报数后,学生总人数减少2,但编号之和不变.
(2)若![]() ,经过
,经过![]() 次
次![]() 循环报数后产生
循环报数后产生![]() 个新编号,这些编号之和为
个新编号,这些编号之和为![]() ;再经过
;再经过![]() 次循环报数产生
次循环报数产生![]() 个新编号,这些编号之和也为
个新编号,这些编号之和也为![]() ;……经过共
;……经过共![]()
次循环报数,最后剩下1名学生,他的编号为![]() ,且他的原始编号为
,且他的原始编号为![]() (即当
(即当![]() 时,最后一名学生留在场上).
时,最后一名学生留在场上).
由(1)知![]() .
.
(3)若一圈学生人数为![]() ,且最后一名学生的编号为
,且最后一名学生的编号为![]() ,则经过
,则经过![]() 次循环报数后,产生
次循环报数后,产生![]() 个新编号,此时,学生人数变为
个新编号,此时,学生人数变为![]() ,第1名学生编号为
,第1名学生编号为![]() .
.
对于一般的奇数![]() ,令
,令![]() ,
,![]() 满足
满足![]() .
.
则![]() ,
,![]() .
.
首先,前![]() 名学生
名学生![]() ,
,![]() ,…,
,…,![]() 称为第一组,其编号和为
称为第一组,其编号和为![]() .
.
记学生初始编号和![]() .
.
由(1)、(3)知,经过![]() 次
次![]() 循环报数,学生人数变为
循环报数,学生人数变为![]() ,其中,第一名学生编号为
,其中,第一名学生编号为![]() 称为第二组;再经过
称为第二组;再经过![]() 次循环报数后,学生人数变为
次循环报数后,学生人数变为![]() ,称为第三组;重复循环报数直到学生人数为1,此时,是第
,称为第三组;重复循环报数直到学生人数为1,此时,是第![]() 组.
组.
最后留在场上的学生原始编号为![]() ,且
,且![]() .
.
当![]() 时,因
时,因![]() ,所以,
,所以,![]() ,
,![]() .
.
最后留在场上的学生原始编号为l923.故![]() .
.

【题目】经观测,某昆虫的产卵数![]() 与温度
与温度![]() 有关,现将收集到的温度
有关,现将收集到的温度![]() 和产卵数
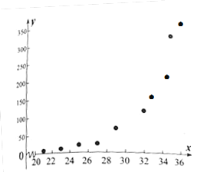
和产卵数![]() 的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
|
|
|
|
|
|
275 | 731.1 | 21.7 | 150 | 2368.36 | 30 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() ,
,![]() 与
与![]() 哪一个适宜作为
哪一个适宜作为![]() 与
与![]() 之间的回归方程模型?(给出判断即可,不必说明理由)
之间的回归方程模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据.
①试求![]() 关于
关于![]() 回归方程;
回归方程;
②已知用人工培养该昆虫的成本![]() 与温度
与温度![]() 和产卵数
和产卵数![]() 的关系为
的关系为![]() ,当温度
,当温度![]() (
(![]() 取整数)为何值时,培养成本的预报值最小?
取整数)为何值时,培养成本的预报值最小?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为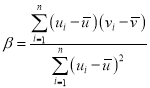 ,
,![]() .
.
【题目】若无穷数列![]() 满足:
满足:![]() ,当
,当![]() ,
,![]() 时.
时.
![]() 其中
其中![]() 表示
表示![]() ,
,![]() ,
,![]() ,
,![]() 中的最大项
中的最大项![]() ,有以下结论:
,有以下结论:
![]() 若数列
若数列![]() 是常数列,则
是常数列,则![]()
![]() 若数列
若数列![]() 是公差
是公差![]() 的等差数列,则
的等差数列,则![]() ;
;
![]() 若数列
若数列![]() 是公比为q的等比数列,则
是公比为q的等比数列,则![]()
则其中正确的结论是______![]() 写出所有正确结论的序号
写出所有正确结论的序号![]()
【题目】某水果经销商为了对一批刚上市水果进行合理定价,将该水果按事先拟定的价格进行试销,得到一组销售数据,如表所示:
试销单价 | 16 | 17 | 18 | 19 | 20 |
日销售量 | 168 | 146 | 120 | 90 | 56 |
(1)已知变量![]() 具有线性相关关系,求该水果日销售量
具有线性相关关系,求该水果日销售量![]() (公斤)关于试销单价
(公斤)关于试销单价![]() (元/公斤)的线性回归方程,并据此分析销售单价
(元/公斤)的线性回归方程,并据此分析销售单价![]() 时,日销售量的变化情况;
时,日销售量的变化情况;
(2)若该水果进价为每公斤![]() 元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价
元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价![]()
![]() 应定为多少元?
应定为多少元?
(参考数据及公式:![]() ,
,![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,
,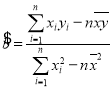 ,
,![]() )
)
