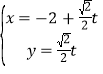题目内容
【题目】经观测,某昆虫的产卵数![]() 与温度
与温度![]() 有关,现将收集到的温度
有关,现将收集到的温度![]() 和产卵数
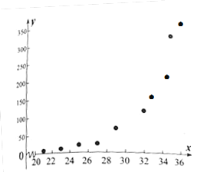
和产卵数![]() 的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
|
|
|
|
|
|
275 | 731.1 | 21.7 | 150 | 2368.36 | 30 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() ,
,![]() 与
与![]() 哪一个适宜作为
哪一个适宜作为![]() 与
与![]() 之间的回归方程模型?(给出判断即可,不必说明理由)
之间的回归方程模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据.
①试求![]() 关于
关于![]() 回归方程;
回归方程;
②已知用人工培养该昆虫的成本![]() 与温度
与温度![]() 和产卵数
和产卵数![]() 的关系为
的关系为![]() ,当温度
,当温度![]() (
(![]() 取整数)为何值时,培养成本的预报值最小?
取整数)为何值时,培养成本的预报值最小?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为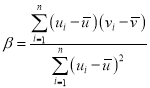 ,
,![]() .
.
【答案】(1)![]() 更适宜;(2)①
更适宜;(2)①![]() ;②14.
;②14.
【解析】
(1)根据样本点分布在一条指数函数的周围,可确定适宜的回归模型.
(2)①令![]() 则
则![]() ,根据已知数据求出
,根据已知数据求出![]() ,得回归模型;②由①得
,得回归模型;②由①得![]() ,由二次函数性质得最小值.
,由二次函数性质得最小值.
解:(1)根据散点图判断,看出样本点分布在一条指数函数的周围,所以![]() 适宜作为
适宜作为![]() 与
与![]() 之间的回归方程模型;
之间的回归方程模型;
(2)①令![]() 则
则![]()
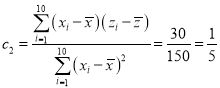
![]()
![]()
∴![]()
②![]()
∴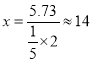 时,培养成本的预报值最小.
时,培养成本的预报值最小.

【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从某市移动支付用户中随机抽取100人进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移动支付6次及以上的用户称为“移动支付达人”,按分层抽样的方法,从参与调查的“移动支付达人”中,随机抽取6人,求抽取的6人中,男、女用户各多少人;
(2)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,根据表格中的数据完成下列![]() 列联表,问:能否有
列联表,问:能否有![]() 的把握认为“移动支付活跃用户”与性别有关?
的把握认为“移动支付活跃用户”与性别有关?
非移动支付活跃用户 | 移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 |
附参照表:
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: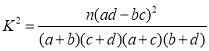 ,其中
,其中![]()