题目内容
设f0(x)=cos x,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈
N,则f2 011(x)等于 ( ).
N,则f2 011(x)等于 ( ).
| A.sin x | B.-sin x |
| C.cos x | D.-cos x |
A
f0(x)=cos x,f1(x)=-sin x,f2(x)=-cos x,
f3(x)=sin x,f4(x)=cos x,…,
由此看出,四个一循环,具有周期性,T=4.∵2 011=4×502+3,∴f2 011(x)=f3(x)=sin x.
f3(x)=sin x,f4(x)=cos x,…,
由此看出,四个一循环,具有周期性,T=4.∵2 011=4×502+3,∴f2 011(x)=f3(x)=sin x.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

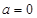 时,求
时,求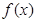 的最小值;
的最小值; >1恒成立,求实数a的取值范围;
>1恒成立,求实数a的取值范围; (其中
(其中 )。
)。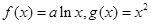 .其中
.其中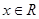 .
.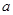 的值;
的值;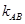 ,若
,若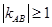 ,求
,求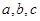 满足
满足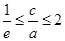 ,
,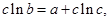 则
则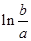 的取值范围是( )
的取值范围是( )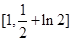
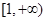
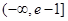
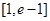
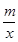 (m∈R)在区间[1,e]上取得最小值4,则m=________.
(m∈R)在区间[1,e]上取得最小值4,则m=________.
 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.