题目内容
已知函数f(x)=lnx-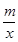 (m∈R)在区间[1,e]上取得最小值4,则m=________.
(m∈R)在区间[1,e]上取得最小值4,则m=________.
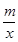 (m∈R)在区间[1,e]上取得最小值4,则m=________.
(m∈R)在区间[1,e]上取得最小值4,则m=________.-3e
f′(x)=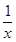 +
+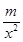 =
=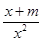 ,令f′(x)=0,则x=-m,且当x<-m时,f′(x)<0,f(x)单调递减,当x>-m时,f′(x)>0,f(x)单调递增.若-m≤1,即m≥-1时,f(x)min=f(1)=-m≤1,不可能等于4;若1<-m≤e,即-e≤m<-1时,f(x)min=f(-m)=ln(-m)+1,令ln(-m)+1=4,得m=-e3?(-e,-1);若-m>e,即m<-e时,f(x)min=f(e)=1-
,令f′(x)=0,则x=-m,且当x<-m时,f′(x)<0,f(x)单调递减,当x>-m时,f′(x)>0,f(x)单调递增.若-m≤1,即m≥-1时,f(x)min=f(1)=-m≤1,不可能等于4;若1<-m≤e,即-e≤m<-1时,f(x)min=f(-m)=ln(-m)+1,令ln(-m)+1=4,得m=-e3?(-e,-1);若-m>e,即m<-e时,f(x)min=f(e)=1-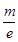 ,令1-
,令1-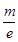 =4,得m=-3e,符合题意.综上所述,m=-3e.
=4,得m=-3e,符合题意.综上所述,m=-3e.
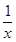 +
+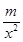 =
=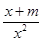 ,令f′(x)=0,则x=-m,且当x<-m时,f′(x)<0,f(x)单调递减,当x>-m时,f′(x)>0,f(x)单调递增.若-m≤1,即m≥-1时,f(x)min=f(1)=-m≤1,不可能等于4;若1<-m≤e,即-e≤m<-1时,f(x)min=f(-m)=ln(-m)+1,令ln(-m)+1=4,得m=-e3?(-e,-1);若-m>e,即m<-e时,f(x)min=f(e)=1-
,令f′(x)=0,则x=-m,且当x<-m时,f′(x)<0,f(x)单调递减,当x>-m时,f′(x)>0,f(x)单调递增.若-m≤1,即m≥-1时,f(x)min=f(1)=-m≤1,不可能等于4;若1<-m≤e,即-e≤m<-1时,f(x)min=f(-m)=ln(-m)+1,令ln(-m)+1=4,得m=-e3?(-e,-1);若-m>e,即m<-e时,f(x)min=f(e)=1-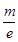 ,令1-
,令1-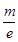 =4,得m=-3e,符合题意.综上所述,m=-3e.
=4,得m=-3e,符合题意.综上所述,m=-3e.
练习册系列答案
相关题目
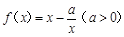 ,
,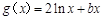 ,且直线
,且直线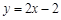 与曲线
与曲线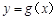 相切.
相切.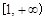 内的一切实数
内的一切实数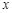 ,不等式
,不等式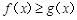 恒成立,求实数
恒成立,求实数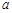 的取值范围;
的取值范围;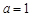 时,求最大的正整数
时,求最大的正整数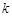 ,使得对
,使得对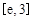 (
(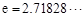 是自然对数的底数)内的任意
是自然对数的底数)内的任意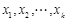 都有
都有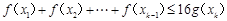 成立;
成立;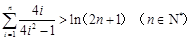 .
.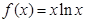 ,
,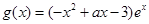 (a为实数).
(a为实数).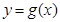 在
在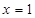 处的切线方程;
处的切线方程;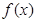 在区间
在区间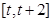 (
(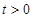 )上的最小值;
)上的最小值;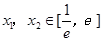 ,使方程
,使方程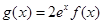 成立,求实数a的取值范围.
成立,求实数a的取值范围.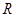 上的函数
上的函数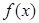 满足:
满足: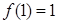 ,且对于任意的
,且对于任意的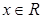 ,都有
,都有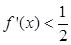 ,则不等式
,则不等式 的解集为 __________________.
的解集为 __________________.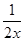 -cosx,若
-cosx,若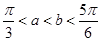 ,则( )
,则( )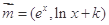 ,
,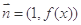 ,
,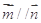 (
(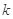 为常数,
为常数, 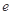 是自然对数的底数),曲线
是自然对数的底数),曲线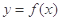 在点
在点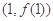 处的切线与
处的切线与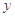 轴垂直,
轴垂直,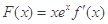 .
.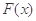 的单调区间;
的单调区间;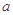 为正实数),若对于任意
为正实数),若对于任意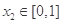 ,总存在
,总存在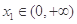 , 使得
, 使得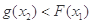 ,求实数
,求实数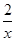 -3ln x,其中a为常数.
-3ln x,其中a为常数.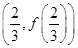 处的切线的斜率为1时,求函数f(x)在
处的切线的斜率为1时,求函数f(x)在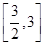 上的最小值;
上的最小值;