题目内容
设函数f(x)=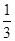 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.
(1)试问函数f(x)能否在x=-1时取得极值?说明理由;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
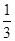 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.(1)试问函数f(x)能否在x=-1时取得极值?说明理由;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
(1)无极值(2)-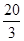 <c<
<c<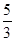 或c=-9.
或c=-9.
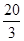 <c<
<c<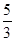 或c=-9.
或c=-9.(1)由题意f′(x)=x2-2ax-a,
假设在x=-1时f(x)取得极值,则有f′(-1)=(-1)2-2a(-1)-a=0,解得a=-1.
而此时f′(x)=x2+2x+1=(x+1)2≥0,所以函数f(x)在R上为增函数,函数无极值.
这与f(x)在x=-1处有极值矛盾,所以f(x)在x=-1处无极值.
(2)设f(x)=g(x),则有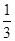 x3-ax2-ax=2x2+4x+c,
x3-ax2-ax=2x2+4x+c,
所以c=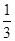 x3-x2-3x.
x3-x2-3x.
设F(x)=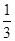 x3-x2-3x,则F′(x)=x2-2x-3,令F′(x)=0,解得x1=-1,x2=3.
x3-x2-3x,则F′(x)=x2-2x-3,令F′(x)=0,解得x1=-1,x2=3.
当x变化时,F′(x),F(x)的变化情况如表所示:
由表可知F(x)在[-3,-1],[3,4]上是增函数,在[-1,3]上是减函数.
当x=-1时,F(x)取得极大值F(-1)=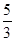 ;当x=3时,F(x)取得极小值F(3)=-9,而F(-3)=-9,F(4)=-
;当x=3时,F(x)取得极小值F(3)=-9,而F(-3)=-9,F(4)=-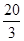 .
.
如果函数f(x)与g(x)的图象有两个公共点,则函数F(x)与y=c有两个公共点,所以-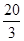 <c<
<c<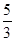 或c=-9.
或c=-9.
假设在x=-1时f(x)取得极值,则有f′(-1)=(-1)2-2a(-1)-a=0,解得a=-1.
而此时f′(x)=x2+2x+1=(x+1)2≥0,所以函数f(x)在R上为增函数,函数无极值.
这与f(x)在x=-1处有极值矛盾,所以f(x)在x=-1处无极值.
(2)设f(x)=g(x),则有
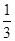 x3-ax2-ax=2x2+4x+c,
x3-ax2-ax=2x2+4x+c,所以c=
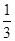 x3-x2-3x.
x3-x2-3x.设F(x)=
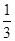 x3-x2-3x,则F′(x)=x2-2x-3,令F′(x)=0,解得x1=-1,x2=3.
x3-x2-3x,则F′(x)=x2-2x-3,令F′(x)=0,解得x1=-1,x2=3.当x变化时,F′(x),F(x)的变化情况如表所示:
| x | -3 | (-3,-1) | -1 | (-1,3) | 3 | (3,4) | 4 |
| F′(x) | | + | 0 | - | 0 | + | |
| F(x) | -9 | ? | 极大值 | ? | 极小值 | ? | -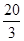 |
当x=-1时,F(x)取得极大值F(-1)=
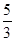 ;当x=3时,F(x)取得极小值F(3)=-9,而F(-3)=-9,F(4)=-
;当x=3时,F(x)取得极小值F(3)=-9,而F(-3)=-9,F(4)=-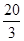 .
.如果函数f(x)与g(x)的图象有两个公共点,则函数F(x)与y=c有两个公共点,所以-
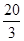 <c<
<c<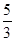 或c=-9.
或c=-9.
练习册系列答案
相关题目
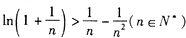
 ,以点
,以点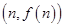 为切点作函数图像的切线
为切点作函数图像的切线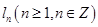 ,直线
,直线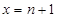 与函数
与函数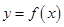 图像及切线
图像及切线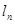 分别相交于
分别相交于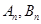 ,记
,记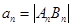 .
.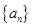 的通项;
的通项;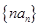 的前
的前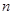 项和为
项和为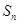 ,求证:
,求证: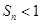 .
.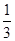 x3-
x3-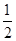 x2+bx的图象在交点(0,0)处有公共切线.
x2+bx的图象在交点(0,0)处有公共切线.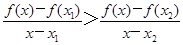 .
.
 是函数
是函数 (
( )的两个极值点
)的两个极值点 ,求函数
,求函数 的解析式;
的解析式; ,求
,求 的最大值。
的最大值。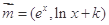 ,
,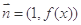 ,
,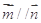 (
(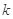 为常数,
为常数, 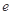 是自然对数的底数),曲线
是自然对数的底数),曲线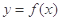 在点
在点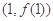 处的切线与
处的切线与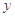 轴垂直,
轴垂直,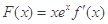 .
.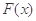 的单调区间;
的单调区间;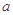 为正实数),若对于任意
为正实数),若对于任意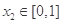 ,总存在
,总存在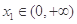 , 使得
, 使得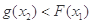 ,求实数
,求实数