题目内容
【题目】(本小题满分12分)
在如图所示的多面体中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1) 解法1

证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() . …………2分
. …………2分
过![]() 作
作![]() 交
交![]() 于
于![]() ,则
,则![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() . …………4分
. …………4分
∵![]() ,∴四边形
,∴四边形![]() 平行四边形,
平行四边形,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴四边形![]() 为正方形,
为正方形,
∴![]() , ……………6分
, ……………6分
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ⊥平面
⊥平面![]() . ………………………7分
. ………………………7分
∵![]() 平面
平面![]() ,
,
∴![]() . ………………………8分
. ………………………8分
(2)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴平面![]() ⊥平面
⊥平面![]()
由(1)可知![]()
∴![]() ⊥平面
⊥平面![]()
∵![]() 平面
平面![]()
∴![]() ……………………9分
……………………9分
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]()
∵四边形![]() 是正方形,
是正方形,
∴![]()
∵![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() ⊥平面
⊥平面![]()
∴![]() ⊥
⊥![]() Z|X|X|K]
Z|X|X|K]
∴![]() 是二面角
是二面角![]() 的平面角, ………………………12分
的平面角, ………………………12分
由计算得![]()
∴![]() ………………………13分
………………………13分
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .………………………14分
.………………………14分
解法2
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,
,
又![]() ,
,
∴![]() 两两垂直. ……………………2分
两两垂直. ……………………2分
以点E为坐标原点,![]() 分别为
分别为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.

由已知得,![]() (0,0,2),
(0,0,2),![]() (2,0,0),
(2,0,0),
![]() (2,4,0),
(2,4,0),![]() (0,3,0),
(0,3,0),![]() (0,2,2),
(0,2,2),
![]() (2,2,0). …………………………4分
(2,2,0). …………………………4分
∴![]() ,
,![]() ,………6分
,………6分
∴![]() , ………7分
, ………7分
∴![]() . …………………………8分
. …………………………8分
(2)由已知得![]() 是平面
是平面![]() 的法向量. ………………………9分
的法向量. ………………………9分
设平面![]() 的法向量为
的法向量为![]() ,
,
∵![]() ,
,
∴ ,即
,即![]() ,令
,令![]() ,得
,得![]() . ……………12分
. ……………12分
设平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,
,
则![]() …………………………13分
…………………………13分
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() . …………………………14分
. …………………………14分
【解析】
(1)证明EB,EF,EA两两垂直,以点E为坐标原点,EB,EF,EA分别为x,y,z轴,建立空间直角坐标系用坐标表示点与向量,证明
![]() ,可得BD⊥EG;
,可得BD⊥EG;
(2)由已知得![]() 是平面DEF的法向量,求出平面DEG的法向量
是平面DEF的法向量,求出平面DEG的法向量
![]() ,利用向量的夹角公式,可求平面DEG与平面DEF所成锐二面角的余弦值.
,利用向量的夹角公式,可求平面DEG与平面DEF所成锐二面角的余弦值.
(Ⅰ)![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .又
.又![]() ,
,
![]() BE,EF,AE两两垂直.
BE,EF,AE两两垂直.
以点E为坐标原点,EB,EF,EA分别为x,y,z轴,
建立空间直角坐标系,
由已知得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() .
.
(Ⅱ)由已知得![]() 是平面DEF的法向量,
是平面DEF的法向量,
设平面的DEG法向量为![]() ,
,
![]() ,
,![]() ,
,
 即
即![]() 令
令![]() ,得
,得![]() ,
,
设平面DEG与平面DEF所成锐二面角的大小为θ,
则 .
.
![]() 平面DEG与平面DEF所成锐二面角的余弦值为
平面DEG与平面DEF所成锐二面角的余弦值为![]() .
.

 期末集结号系列答案
期末集结号系列答案【题目】“互联网![]() ”是“智慧城市”的重要内士,
”是“智慧城市”的重要内士,![]() 市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费
市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费![]() .为了解免费
.为了解免费![]() 在
在![]() 市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了
市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了![]() 人进行抽样分析,得到如下列联表(单位:人):
人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有![]() 的把握认为
的把握认为![]() 市使用免费
市使用免费![]() 的情况与年龄有关;
的情况与年龄有关;
(2)将频率视为概率,现从该市![]() 岁以上的市民中用随机抽样的方法每次抽取
岁以上的市民中用随机抽样的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.记被抽取的
次.记被抽取的![]() 人中“偶尔或不用免费
人中“偶尔或不用免费![]() ”的人数为
”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,数学期望
的分布列,数学期望![]() 和方差
和方差![]() .
.
附: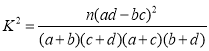 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |