题目内容
已知函数f(x)＝x3－12x＋a，其中a≥16，则下列说法正确的是( )．
| A．f(x)有且只有一个零点 |
| B．f(x)至少有两个零点 |
| C．f(x)最多有两个零点 |
| D．f(x)一定有三个零点 |
C
f′(x)＝3x2－12，令f′(x)>0得x>2或x<－2，令f′(x)<0得－2<x<2.所以f(x)在(－∞，－2)和(2，＋∞)上单调递增，在(－2,2)上单调递减，故f(x)的极大值为f(－2)＝16＋a，f(x)的极小值为f(2)＝－16＋a，又a≥16.所以f(2)≥0，故f(x)最多有两个零点．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
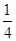
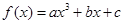图像过点
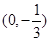，且在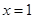
处的切线方程是
.
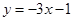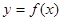的解析式；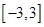
上的最大值和最小值．
在x＝2处的切线斜率为________．
.若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格)．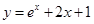
在点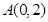
处的切线方程 .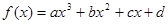
，给出定义：
是函数
的导函数，
是
有实数解
，则称点
为函数
的“拐点”.某同学经研究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且拐点就是对称中心.若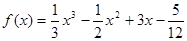
，请你根据这一发现，求：（1）函数
=________.
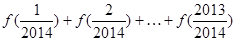，则切点坐标为________．