题目内容
已知函数f(x)=ln x+2x-6.
(1)证明:函数f(x)有且只有一个零点;
(2)求该零点所在的一个区间,使这个区间的长度不超过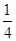
(1)证明:函数f(x)有且只有一个零点;
(2)求该零点所在的一个区间,使这个区间的长度不超过
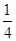
(1)见解析(2)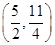
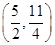
(1)f(x)的定义域为(0,+∞),且f(x)是增函数.
∵f(2)=ln 2-2<0,f(3)=ln 3>0,
∴f(2)·f(3)<0.
∴f(x)在(2,3)上至少有一个零点.
又因f(x)在(0,+∞)上是增函数,
从而f(x)在(0,+∞)上有且只有一个零点.
(2)由(1)知f(2)<0,f(3)>0.
∴f(x)的零点x0∈(2,3).
取x1=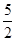 ,∵f
,∵f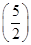 =ln
=ln 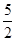 -1=ln
-1=ln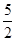 -ln e<0,∴f
-ln e<0,∴f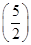 ·f(3)<0,∴x0∈
·f(3)<0,∴x0∈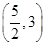 .
.
取x2=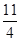 ,∵f
,∵f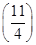 =ln
=ln 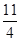 -
-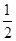 =ln
=ln 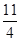 -ln e
-ln e 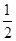 >0,∴f
>0,∴f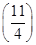 ·f
·f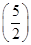 <0.
<0.
∴x0∈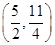 且
且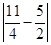 =
=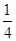 ≤
≤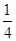 ,∴
,∴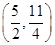 即为符合条件的区间.
即为符合条件的区间.
∵f(2)=ln 2-2<0,f(3)=ln 3>0,
∴f(2)·f(3)<0.
∴f(x)在(2,3)上至少有一个零点.
又因f(x)在(0,+∞)上是增函数,
从而f(x)在(0,+∞)上有且只有一个零点.
(2)由(1)知f(2)<0,f(3)>0.
∴f(x)的零点x0∈(2,3).
取x1=
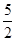 ,∵f
,∵f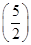 =ln
=ln 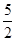 -1=ln
-1=ln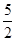 -ln e<0,∴f
-ln e<0,∴f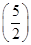 ·f(3)<0,∴x0∈
·f(3)<0,∴x0∈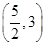 .
.取x2=
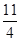 ,∵f
,∵f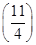 =ln
=ln 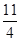 -
-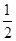 =ln
=ln 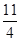 -ln e
-ln e 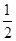 >0,∴f
>0,∴f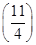 ·f
·f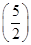 <0.
<0.∴x0∈
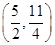 且
且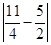 =
=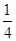 ≤
≤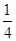 ,∴
,∴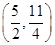 即为符合条件的区间.
即为符合条件的区间.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 x3+
x3+ x2-2x(a∈R).
x2-2x(a∈R).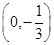 可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.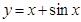 在点
在点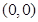 处的切线方程是 .
处的切线方程是 .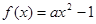 的图像在点A(1,f(1))处的切线l与直线
的图像在点A(1,f(1))处的切线l与直线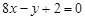 平行,若数列
平行,若数列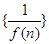 的前
的前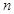 项和为
项和为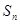 ,则
,则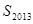 的值为( )
的值为( )




 交于点P,若设曲线y=f(x)在点P处的切线与x轴交点的横坐标为
交于点P,若设曲线y=f(x)在点P处的切线与x轴交点的横坐标为 的值为 .
的值为 .