题目内容
若定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则有( )
| A、f(-25)<f(80)<f(11) |
| B、f(11)<f(80)<f(-25) |
| C、f(-25)<f(11)<f(80) |
| D、f(80)<f(11)<f(-25) |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系,即可得到结论.
解答:
解:∵定义在R上的奇函数f(x)满足f(x-4)=-f(x),
∴f(x-4)=-f(x)=f(-x),
则函数关于x=-2和x=2对称,
且f(-x-4)=-f(-x),
即-f(x+4)=f(x),则f(x+8)=-f(x+4)=f(x),
则f(-25)=f(-1)=-f(1)
f(80)=f(0),
f(11)=f(3)=-f(-1)=f(1)
又∵函数在区间[0,2]上是增函数
0=f(0)<f(1)
∴-f(1)<f(0)<f(1)
∴f(-25)<f(80)<f(11)
故选:A
∴f(x-4)=-f(x)=f(-x),
则函数关于x=-2和x=2对称,
且f(-x-4)=-f(-x),
即-f(x+4)=f(x),则f(x+8)=-f(x+4)=f(x),
则f(-25)=f(-1)=-f(1)
f(80)=f(0),
f(11)=f(3)=-f(-1)=f(1)
又∵函数在区间[0,2]上是增函数
0=f(0)<f(1)
∴-f(1)<f(0)<f(1)
∴f(-25)<f(80)<f(11)
故选:A
点评:本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
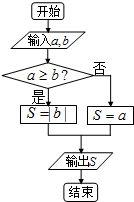 定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )
定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )| A、2 | B、-1 | C、4 | D、3 |
P:x≥3或x≤1,Q:x2-3x+2≥0,则“非P”是“非Q”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
有一半径为4的圆,现将一枚直径为2的硬币投向其中(硬币与圆面有公共点就算是有效试验,硬币完全落在圆外的不计),则硬币完全落入圆内的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={y|y=log3x,x>1},B={y|y=(
)x,x>1},则A∩B=( )
| 1 |
| 3 |
A、{y |0<y<
| ||
| B、{y|0<y<1} | ||
C、{y |
| ||
| D、∅ |