题目内容
函数y=
的定义域为 ．
| 3-x-x2 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：利用偶次方被开放数非负，解二次不等式即可得到函数的定义域．
解答：
解：要使函数函数y=
有意义，必有：3-x-x2≥0，解得x∈[
，
]．
故答案为：[
，
]．
| 3-x-x2 |
-1-
| ||
| 2 |
-1+
| ||
| 2 |
故答案为：[
-1-
| ||
| 2 |
-1+
| ||
| 2 |
点评：本题考查函数的定义域的求法，二次不等式的解法，基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
P：x≥3或x≤1，Q：x2-3x+2≥0，则“非P”是“非Q”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知集合A={y|y=log3x，x＞1}，B={y|y=(
)x，x＞1}，则A∩B=（ ）
| 1 |
| 3 |
A、{y |0＜y＜
| ||
| B、{y|0＜y＜1} | ||
C、{y |
| ||
| D、∅ |
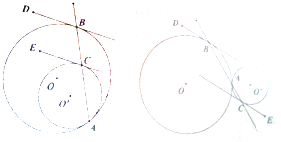已知：如图，⊙O和⊙O′相切于点A，直线AB和⊙O的另一个交点为B，和⊙O′的另一个交点为C，BD，CE分别切⊙O′，⊙O于点B，C．求证：BD∥CE．研究：两圆外切时结论还成立吗？