题目内容
已知数列 的前n项和为
的前n项和为 ,且
,且
(1)求数列 的通项公式;
的通项公式;
(2)若 满足
满足 ,求数列
,求数列 的前n项和为
的前n项和为 ;
;
(3)设 是数列
是数列 的前n项和,求证:
的前n项和,求证: 。
。
 的前n项和为
的前n项和为 ,且
,且
(1)求数列
 的通项公式;
的通项公式;(2)若
 满足
满足 ,求数列
,求数列 的前n项和为
的前n项和为 ;
;(3)设
 是数列
是数列 的前n项和,求证:
的前n项和,求证: 。
。(1) ;(2)
;(2) ;(3)见解析。
;(3)见解析。
 ;(2)
;(2) ;(3)见解析。
;(3)见解析。试题分析:(1)利用
 可求得数列
可求得数列 的通项公式,注意验证
的通项公式,注意验证 ;(2)由(1)知
;(2)由(1)知 ,即数列
,即数列 为等比数列,利用其前n项和公式进行求和;(3)利用裂项相消求得
为等比数列,利用其前n项和公式进行求和;(3)利用裂项相消求得 ,再利用函数的单调性可得证。
,再利用函数的单调性可得证。(1)当
 时,
时, ,
, 当
 时,
时, ,也适合上式.
,也适合上式.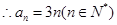 。
。(2)
 ,
,
(3)
 ,
, 
 单调递增,
单调递增, 故
故
 求数列的通项公式;(2)等比数列前其前n项和公式的应用;(3)利用裂项相消进行数列求和。
求数列的通项公式;(2)等比数列前其前n项和公式的应用;(3)利用裂项相消进行数列求和。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前
的前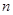 项和为
项和为 ,满足
,满足 ,
, ,且
,且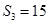 .
. 、
、 、
、 的值;
的值; 的通项公式.
的通项公式. 中,若
中,若 ,
, ,则
,则 .
. =( )
=( )

 (i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如
(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如 =8,则
=8,则 为 。
为 。
 的前n项和为
的前n项和为 ,
, ,则数列
,则数列 的前100项和为________.
的前100项和为________. <-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为________.
<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为________.