题目内容
设数列 的前
的前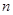 项和为
项和为 ,满足
,满足 ,
, ,且
,且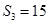 .
.
(1)求 、
、 、
、 的值;
的值;
(2)求数列 的通项公式.
的通项公式.
 的前
的前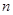 项和为
项和为 ,满足
,满足 ,
, ,且
,且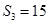 .
.(1)求
 、
、 、
、 的值;
的值;(2)求数列
 的通项公式.
的通项公式.(1)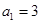 ,
,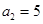 ,
,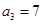 ;(2)
;(2)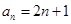 .
.
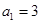 ,
,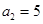 ,
,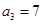 ;(2)
;(2)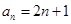 .
.试题分析:(1)由
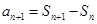 代入
代入 ,得到
,得到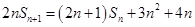 ,然后由
,然后由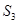 的值逐步算出
的值逐步算出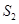 与
与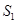 的值,然后利用
的值,然后利用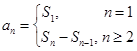 求出
求出 、
、 、
、 的值;(2)利用(1)中的结论归纳出
的值;(2)利用(1)中的结论归纳出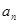 的通项公式,并以此归纳出
的通项公式,并以此归纳出 的表达式,然后利用数学归纳法证明数列
的表达式,然后利用数学归纳法证明数列 的通项公式的正确性.
的通项公式的正确性.试题解析:(1)由
 得
得 ,
,整理得
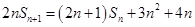 ,因此有
,因此有 ,
,即
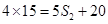 ,解得
,解得 ,
,同理有
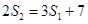 ,即
,即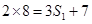 ,解得
,解得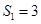 ,
,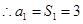 ,
,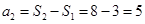 ,
, ;
;(2)由题意得
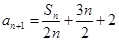 ,
,由(1)知
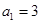 ,
,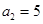 ,
,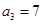 ,猜想
,猜想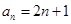 ,
,假设当
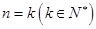 时,猜想成立,即
时,猜想成立,即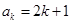 ,则有
,则有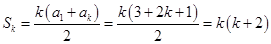 ,
,则当
 时,有
时,有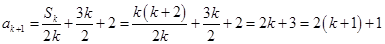 ,
,这说明当
 时,猜想也成立,
时,猜想也成立,由归纳原理知,对任意
 ,
,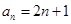 .
.【考点定位】本题考查利用
 与
与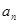 的关系来考查数列的通项的求解,主要考查数学归纳法的应用,属于中等题.
的关系来考查数列的通项的求解,主要考查数学归纳法的应用,属于中等题.
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且
 满足
满足 ,求数列
,求数列 的前n项和为
的前n项和为 ;
; 是数列
是数列 的前n项和,求证:
的前n项和,求证: 。
。 是递增的等差数列,
是递增的等差数列, ,
, 是方程
是方程 的根。
的根。 的前
的前 项和.
项和. 的前
的前 项和为
项和为 ,
, ,
, ,
, ,其中
,其中 为常数,
为常数, ;
;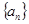 和
和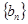 满足
满足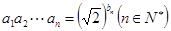 .若
.若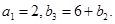
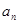 与
与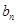 ;
;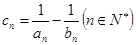 。记数列
。记数列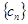 的前
的前 项和为
项和为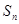 .
.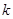 ,使得对任意
,使得对任意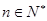 ,均有
,均有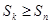 .
.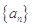 的首项
的首项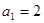 ,且对任意
,且对任意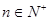 都有
都有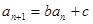 (其中
(其中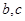 为常数).
为常数).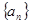 为等差数列,且
为等差数列,且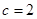 ,求
,求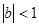 ,从数列
,从数列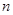 项和
项和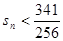 成立的
成立的 是首项为
是首项为 ,公差为
,公差为 的等差数列,
的等差数列, 为其前n项和,若
为其前n项和,若 成等比数列,则
成等比数列,则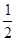

 的前
的前 项和为
项和为 ,且
,且 ,则
,则 ______.
______.