题目内容
【题目】已知圆
，点
，以线段
为直径的圆内切于圆
，记点
的轨迹为
．
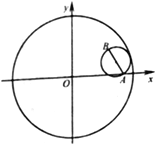
（1）求曲线的方程；
（2）直线交圆于
，
两点，当为
的中点时，求直线的方程．
【答案】（1）
；（2）
或
.
【解析】
试题本题主要考查椭圆的标准方程和几何性质、直线的标准方程和几何性质等基础知识，意在考查考生的分析问题解决问题的能力、读图能力、运算求解能力. 第一问，设AB的中点为M，切点为N，连OM，MN，先利用半径长得出|OM|＋|MN|＝2，再利用中位线转化边，得|AB|＋|AB|＝2(|OM|＋|MN|)＝4，得到椭圆的定义，从而得到a，b，c的值，写出椭圆的方程；第二问，利用OB⊥CD，利用向量垂直的充要条件，得到坐标关系，再结合椭圆方程，可解出
，从而得到直线AB的斜率，得到直线AB的方程.
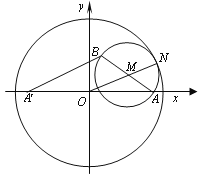
试题解析：（Ⅰ）设AB的中点为M，切点为N，连OM，MN，则
|OM|＋|MN|＝|ON|＝2，取A关于y轴的对称点A，
连AB，故|AB|＋|AB|＝2(|OM|＋|MN|)＝4．
所以点B的轨迹是以A，A为焦点，长轴长为4的椭圆．
其中，a＝2，
，b＝1，则
曲线Γ的方程为． 5分
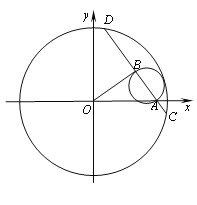
（Ⅱ）因为B为CD的中点，所以OB⊥CD，
则
．设B(x0，y0)，
则
． 7分
又
解得
，
．
则kOB＝
，kAB＝
， 10分
则直线AB的方程为
，即
或． 12分
【题目】我国城市空气污染指数范围及相应的空气质量类别见下表：
空气污染指数 | 空气质量 | 空气污染指数 | 空气质量 | |
0--50 | 优 | 201--250 | 中度污染 | |
51--100 | 良 | 251--300 | 中度重污染 | |
101--150 | 轻微污染 | >300 | 重污染 | |
151----200 | 轻度污染 |
我们把某天的空气污染指数在0-100时称作A类天，101--200时称作B类天，大于200时称作C类天．下图是某市2014年全年监测数据中随机抽取的18天数据作为样本，其茎叶图如下：（百位为茎，十.个位为叶）
（1）从这18天中任取3天，求至少含2个A类天的概率；
（2）从这18天中任取3天，记X是达到A类或B类天的天数，求X的分布列及数学期望．
