题目内容

【题目】某射击运动员进行射击训练，前三次射击在靶上的着弹点刚好是边长为的等边三角形的三个顶点.

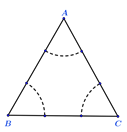
（Ⅰ）第四次射击时，该运动员瞄准区域射击（不会打到外），则此次射击的着弹点距的距离都超过的概率为多少？（弹孔大小忽略不计）

(Ⅱ) 该运动员前三次射击的成绩（环数）都在区间内，调整一下后，又连打三枪，其成绩（环数）都在区间内.现从这次射击成绩中随机抽取两次射击的成绩（记为和）进行技术分析.求事件“”的概率.

【答案】(I)1-(II)

【解析】

（I）用三角形的面积减去三个扇形的面积，得到“着弹点距的距离都超过”的点的面积，用这个面积除以三角形的面积得到所求的概率.（II）利用列举法列出所有的基本事件，进而得到符合题意的事件，利用古典概型概率计算公式，求得所求的概率.

（Ⅰ）因为着弹点若与的距离都超过cm，

则着弹点就不能落在分别以为中心,半径为cm的三个扇形区域内，

只能落在图中阴影部分内.

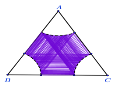
因为

图中阴影部分的面积为，

故所求概率为

（Ⅱ）前三次射击成绩依次记为，后三次成绩依次记为，从这次射击成绩中随机抽取两个，基本事件是：

，共个，其中可使发生的是后个基本事件.故.

练习册系列答案
相关题目

【题目】下列命题中，真命题是（ ）

A. 设，则为实数的充要条件是为共轭复数；

B. “直线与曲线C相切”是“直线与曲线C只有一个公共点”的充分不必要条件；

C. “若两直线，则它们的斜率之积等于”的逆命题；

D. 是R上的可导函数，“若是的极值点，则”的否命题．

【题目】德国数学家科拉茨1937年提出一个著名的猜想：任给一个正整数，如果是偶数，就将它减半(即)；如果是奇数，则将它乘3加1(即)，不断重复这样的运算,经过有限步后，一定可以得到1.对于科拉茨猜想，目前谁也不能证明,也不能否定.现在请你研究:如果对正整数(首项)按照上述规则进行变换后的第9项为1(注：1可以多次出现),则的所有不同值的个数为（ ）

A. 4 B. 5 C. 6 D. 7

【题目】青少年“心理健康”问题越来越引起社会关注，某校对高一600名学生进行了一次“心理健康”知识测试，并从中抽取了部分学生的成绩（得分取正整数，满分100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图。

分组

频数

频率

[50,60）

2

0.04

[60,70）

8

0.16

[70,80）

10

[80,90）

[90,100]

14

0.28

合计

1.00

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

（1）填写答题卡频率分布表中的空格，补全频率分布直方图，并标出每个小矩形对应的纵轴数据；

（2）请你估算学生成绩的平均数及中位数。

【题目】已知在中，，且.

（1）求角的大小；

（2）设数列满足，前项和为，若，求的值.

【答案】(1)；(2)或.

【解析】试题分析：

(1)由题意结合三角形内角和为可得.由余弦定理可得，，结合勾股定理可知为直角三角形，，.

(2)结合(1)中的结论可得 .则 ，据此可得关于实数k的方程，解方程可得，则或.

试题解析：

（1）由已知，又，所以.又由，

所以，所以，

所以为直角三角形，，.

（2） .

所以 ，由，得

，所以，所以，所以或.

【题型】解答题
【结束】
18

【题目】已知点是平行四边形所在平面外一点，如果，，.（1）求证：是平面的法向量；

（2）求平行四边形的面积.

【题目】已知圆，点，直线.

（1）求与圆相切，且与直线垂直的直线方程；

（2）在直线上（为坐标原点），存在定点（不同于点），满足：对于圆上任一点，都有为一常数，试求所有满足条件的点的坐标.

【答案】(1)；(2)答案见解析.

【解析】试题分析：

（1）设所求直线方程为，利用圆心到直线的距离等于半径可得关于b的方程，解方程可得，则所求直线方程为

（2）方法1：假设存在这样的点，由题意可得，则，然后证明为常数为即可.

方法2：假设存在这样的点，使得为常数，则，据此得到关于的方程组，求解方程组可得存在点对于圆上任一点，都有为常数.

试题解析：

（1）设所求直线方程为，即，

∵直线与圆相切，∴，得，

∴所求直线方程为

（2）方法1：假设存在这样的点，

当为圆与轴左交点时，；

当为圆与轴右交点时，，

依题意，，解得，（舍去），或.

下面证明点对于圆上任一点，都有为一常数.

设，则，

∴ ，

从而为常数.

方法2：假设存在这样的点，使得为常数，则，

∴，将代入得，

，即

对恒成立，

∴，解得或（舍去），

所以存在点对于圆上任一点，都有为常数.

点睛：求定值问题常见的方法有两种：

(1)从特殊入手，求出定值，再证明这个值与变量无关．

(2)直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．

【题型】解答题
【结束】
22

【题目】已知函数的导函数为，其中为常数.

（1）当时，求的最大值，并推断方程是否有实数解；

（2）若在区间上的最大值为-3，求的值.

【题目】小张经营某一消费品专卖店，已知该消费品的进价为每件40元，该店每月销售量（百件）与销售单价x（元/件）之间的关系用下图的一折线表示，职工每人每月工资为1000元，该店还应交付的其它费用为每月10000元.

（1）把y表示为x的函数；

（2）当销售价为每件50元时，该店正好收支平衡（即利润为零），求该店的职工人数；

（3）若该店只有20名职工，问销售单价定为多少元时，该专卖店可获得最大月利润？（注：利润=收入-支出）

【题目】已知圆 ，点，以线段为直径的圆内切于圆，记点的轨迹为．

（1）求曲线的方程；

（2）直线交圆于，两点，当为的中点时，求直线的方程．

【题目】过圆 ： 上的点 作 轴的垂线，垂足为 ，点 满足 .当 在 上运动时，记点 的轨迹为 .

（1）求 的方程；

（2）过点 的直线 与交于 ， 两点，与圆 交于 ， 两点，求 的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网