题目内容
【题目】已知抛物线![]() 的焦点为F,过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N。
的焦点为F,过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N。
(1)求证:直线MN必过定点;
(2)分别以AB和CD为直径作圆,求两圆相交弦中点H的轨迹方程。
【答案】(1)见解析;(2)![]()
【解析】
(1)易知F(1,0).
设![]() ,代入
,代入![]() ,得
,得![]() .
.
易得![]() ,故
,故![]() .
.
因为CD⊥AB,所以将点M坐标中的k换为![]() ,即得
,即得![]() .
.
则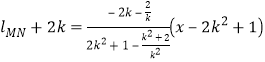 ,
,
即![]() .
.
故不论k为何值,直线MN恒过定点T(3, 0).
(2)由拋物线的性质知,![]() 都与抛物线的准线x=-1相切,所以,
都与抛物线的准线x=-1相切,所以,![]() 的半径分别为
的半径分别为![]() .从而,
.从而,![]() ,
,
![]() .
.
两式相减并整理,得公共弦所在直线方程为![]() .
.
又![]() ,
,
故公共弦所在直线过原点O.
所以,∠OHT=90°.
于是,点H的轨迹是以OT为直径的圆(除去直径的两个端点),其轨迹方程为
![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
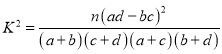 (其中
(其中 ![]() )
)