题目内容
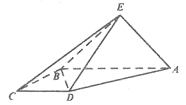
【题目】如图,在底面为正方形的四棱锥![]() 中,
中,![]() 平面
平面![]() ,点
,点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上,且满足
上,且满足![]() ,
,![]() .
.
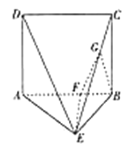
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)在棱![]() 上取一点
上取一点![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() ,可证明
,可证明![]() 是平行四边形,可得
是平行四边形,可得![]() ,由线面平行的判定定理可得结果;(2)以
,由线面平行的判定定理可得结果;(2)以![]() 为坐标原点以
为坐标原点以![]() 为
为![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,利用向量垂直数量积为零列方程求出平面
,利用向量垂直数量积为零列方程求出平面![]() 的法向量,结合平面
的法向量,结合平面![]() 的一个法向量为
的一个法向量为![]() ,利用空间向量夹角余弦公式求解即可.
,利用空间向量夹角余弦公式求解即可.
(1)在棱![]() 上取一点
上取一点![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() .又因为
.又因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
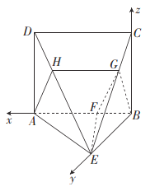
(2)依题意,以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则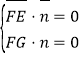 ,即
,即![]() ,取
,取![]() ,
,
则![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以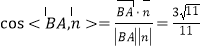 ,
,
又二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分.某市一调查机构针对该市市场占有率最高的甲、乙两家网络外卖企业(以下简称外卖甲,外卖乙)的经营情况进行了调查,调查结果如表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外卖甲日接单 | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单 | 2.2 | 2.3 | 10 | 5 | 15 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(ⅰ)请用相关系数![]() 加以说明:(若
加以说明:(若![]() ,则可认为
,则可认为![]() 与
与![]() 有较强的线性相关关系(
有较强的线性相关关系(![]() 值精确到0.001))
值精确到0.001))
(ⅱ)经计算求得![]() 与
与![]() 之间的回归方程为
之间的回归方程为![]() .假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于2500单时,外卖甲所获取的日纯利润的大致范围:(
.假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于2500单时,外卖甲所获取的日纯利润的大致范围:(![]() 值精确到0.01)
值精确到0.01)
(2)试根据表格中这五天的日接单量情况,从平均值和方差角度说明这两家外卖企业的经营状况.
相关公式:相关系数 ,
,
参考数据:![]()
![]() .
.
【题目】近年来,我国工业经济发展迅速,工业增加值连年攀升,某研究机构统计了近十年(从2008年到2017年)的工业增加值(万亿元),如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工业增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依据表格数据,得到下面的散点图及一些统计量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
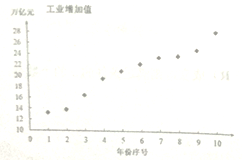
(1)根据散点图和表中数据,此研究机构对工业增加值![]() (万亿元)与年份序号
(万亿元)与年份序号![]() 的回归方程类型进行了拟合实验,研究人员甲采用函数
的回归方程类型进行了拟合实验,研究人员甲采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员乙采用函数
;研究人员乙采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员丙采用线性函数
;研究人员丙采用线性函数![]() ,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数
,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数![]() 与拟合指数
与拟合指数![]() 满足关系
满足关系![]() ).
).
(2)根据(1)的判断结果及统计值,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)预测到哪一年的工业增加值能突破30万亿元大关.
附:样本![]()
![]() 的相关系数
的相关系数 ,
,
![]() ,
,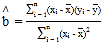 ,
,![]() .
.
【题目】在地面上同一地点观测远方匀速垂直上升的热气球,在上午10点整热气球的仰角是![]() ,到上午10点20分的仰角变成
,到上午10点20分的仰角变成![]() .请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数( )
.请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数( )
|
|
|
|
|
|
|
|
|
|
| 0.5 | 0.559 | 0.629 | 0.643 | 0.656 | 0.669 | 0.682 | 0.695 | 0.707 |
| 0.866 | 0.829 | 0.777 | 0.766 | 0.755 | 0.743 | 0.731 | 0.719 | 0.707 |
| 0.577 | 0.675 | 0.810 | 0.839 | 0.869 | 0.900 | 0.933 | 0.966 | 1.0 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()