题目内容
在正三棱柱ABCA1B1C1中，点D是BC的中点，BC＝BB1.
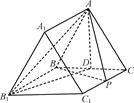
(1)若P是CC1上任一点，求证：AP不可能与平面BCC1B1垂直；
(2)试在棱CC1上找一点M，使MB⊥AB1.
(1)若P是CC1上任一点，求证：AP不可能与平面BCC1B1垂直；
(2)试在棱CC1上找一点M，使MB⊥AB1.
（1）见解析（2）M为CC1的中点
(1)证明：反证法．假设AP⊥平面BCC1B1，
因为BC
平面BCC1B1，所以AP⊥BC.
又正三棱柱ABCA1B1C1中，CC1⊥BC，AP∩CC1＝P，AP平面ACC1A1，CC1平面ACC1A1，所以BC⊥平面ACC1A1.
而AC平面ACC1A1，所以BC⊥AC，这与△ABC是正三角形矛盾．
故AP不可能与平面BCC1B1垂直．
(2)M为CC1的中点．
证明：∵在正三棱柱ABCA1B1C1中，BC＝BB1，∴四边形BCC1B1是正方形．
∵M为CC1的中点，D是BC的中点，∴△B1BD≌△BCM，∴∠BB1D＝∠CBM，∠BDB1＝∠CMB.
∵∠BB1D＋∠BDB1＝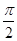
，∠CBM＋∠BDB1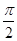＝，∴BM⊥B1D.
∵△ABC是正三角形，D是BC的中点，∴AD⊥BC.
∵平面ABC⊥平面BB1C1C，平面ABC∩平面BB1C1C＝BC，AD平面ABC，
∴AD⊥平面BB1C1C.
∵BM平面BB1C1C，∴AD⊥BM.
∵AD∩B1D＝D，∴BM⊥平面AB1D.
∵AB1平面AB1D，∴MB⊥AB1.
因为BC
平面BCC1B1，所以AP⊥BC.又正三棱柱ABCA1B1C1中，CC1⊥BC，AP∩CC1＝P，AP
平面ACC1A1，CC1平面ACC1A1，所以BC⊥平面ACC1A1.而AC
平面ACC1A1，所以BC⊥AC，这与△ABC是正三角形矛盾．故AP不可能与平面BCC1B1垂直．
(2)M为CC1的中点．
证明：∵在正三棱柱ABCA1B1C1中，BC＝BB1，∴四边形BCC1B1是正方形．
∵M为CC1的中点，D是BC的中点，∴△B1BD≌△BCM，∴∠BB1D＝∠CBM，∠BDB1＝∠CMB.
∵∠BB1D＋∠BDB1＝
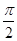，∠CBM＋∠BDB1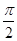＝，∴BM⊥B1D.∵△ABC是正三角形，D是BC的中点，∴AD⊥BC.
∵平面ABC⊥平面BB1C1C，平面ABC∩平面BB1C1C＝BC，AD
平面ABC，∴AD⊥平面BB1C1C.
∵BM
平面BB1C1C，∴AD⊥BM.∵AD∩B1D＝D，∴BM⊥平面AB1D.
∵AB1
平面AB1D，∴MB⊥AB1.
练习册系列答案
相关题目
关于直线
对称，
．把
沿
折起（如图二），使二面角
的余弦值等于
．对于图二，完成以下各小题：
两点间的距离；
平面
；
所成角的正弦值．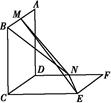
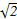.等边三角形ADB以AB为轴转动.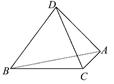
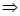β⊥γ”是真命题，如果把α、β、γ中的任意两个换成直线，另一个保持不变，在所得的所有新命题中，真命题的个数是________．
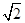，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中，下列说法正确的是________．(填序号)
β；②a∥γ，b∥β；③b∥β，a
γ，且________，则a∥b”为真命题，则可以在横线处填入的条件是________(填序号)．