题目内容
如图一,平面四边形 关于直线
关于直线 对称,
对称,
 .把
.把 沿
沿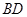 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:

(1)求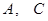 两点间的距离;
两点间的距离;
(2)证明: 平面
平面 ;
;
(3)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 关于直线
关于直线 对称,
对称,
 .把
.把 沿
沿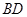 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
(1)求
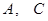 两点间的距离;
两点间的距离;(2)证明:
 平面
平面 ;
;(3)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.(1)2;(2)证明详见解析;(3)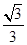 .
.
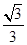 .
.试题分析:(1)取
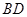 的中点
的中点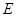 ,先证得
,先证得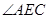 就是二面角
就是二面角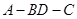 的平面角,再在
的平面角,再在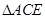 中利用余弦定理即可求得
中利用余弦定理即可求得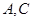 两点间的距离;(2)欲证线面垂直:
两点间的距离;(2)欲证线面垂直: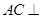 平面
平面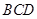 ,转化为证明线线垂直:
,转化为证明线线垂直: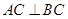 ,
,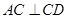 ,即可;(3)欲求直线
,即可;(3)欲求直线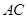 与平面
与平面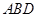 所成角,先结合(1)中的垂直关系作出直线
所成角,先结合(1)中的垂直关系作出直线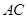 与平面
与平面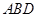 所成角,最后利用直角三角形中的边角关系即可求出所成角的正弦值.
所成角,最后利用直角三角形中的边角关系即可求出所成角的正弦值.试题解析:(1)取
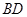 的中点
的中点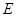 ,连接
,连接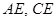 ,
,由
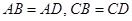 ,得:
,得: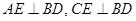 ,
,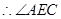 就是二面角
就是二面角 的平面角,
的平面角,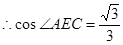 .
.在
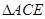 中,
中,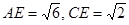
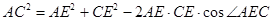
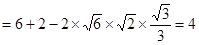
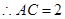 .
.(2)由
 ,
,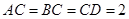 ,
,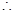
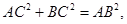
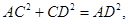
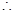
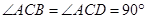 ,
,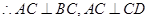 , 又
, 又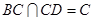
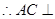 平面
平面 .
.(3)方法一:由(1)知
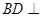 平面
平面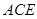
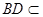 平面
平面
∴平面
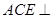 平面
平面 平面
平面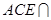 平面
平面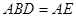 ,
,作
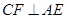 交
交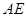 于
于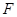 ,则
,则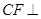 平面
平面 ,
,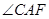 就是
就是 与平面
与平面 所成的角
所成的角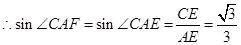 .
.方法二:设点
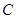 到平面
到平面 的距离为
的距离为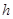 ,
,∵
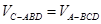
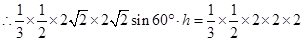
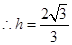 于是
于是 与平面
与平面 所成角
所成角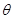 的正弦为
的正弦为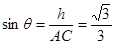 .
. 方法三:以
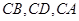 所在直线分别为
所在直线分别为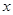 轴,
轴,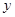 轴和
轴和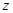 轴建立空间直角坐标系
轴建立空间直角坐标系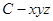 ,
,则
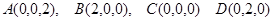 .
.设平面
 的法向量为n
的法向量为n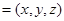 ,则
,则n
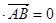 , n
, n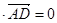 ,
,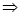
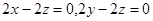
取
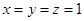 ,则n
,则n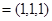 , 于是
, 于是 与平面
与平面 所成角
所成角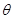 的正弦即
的正弦即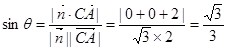 .
.
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 ,
, ,
, ,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转
,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转 ,得到梯形
,得到梯形 .
.
 平面
平面 ;
;  平面
平面 ;
;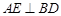 于
于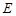 (不同于点
(不同于点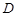 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥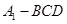 ,如图2所示.
,如图2所示.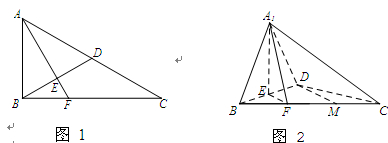
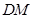 //平面
//平面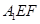 ;
;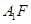 ;
;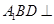 平面
平面 ,试判断直线
,试判断直线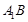 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由. 中,
中, ,斜边
,斜边 .
. 可以通过
可以通过 为轴旋转得到,且二面角
为轴旋转得到,且二面角 是直二面角.动点
是直二面角.动点 在斜边
在斜边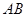 上.
上.
 平面
平面 ;
; 与平面
与平面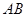 是圆
是圆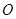 的直径,点
的直径,点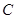 是圆
是圆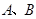 的点,直线
的点,直线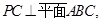
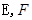 分别为
分别为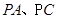 的中点。
的中点。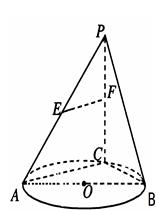
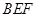 与平面
与平面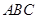 的交线为
的交线为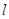 ,试判断
,试判断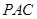 的位置关系,并加以说明;
的位置关系,并加以说明;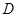 ,且点
,且点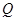 满足
满足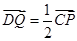 ,记直线
,记直线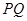
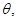 异面直线
异面直线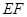 所成的锐角为
所成的锐角为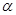 ,二面角
,二面角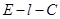 的大小为
的大小为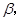
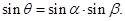
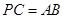 ,求直线
,求直线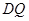 与平面
与平面 ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=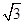 ,BC=4.
,BC=4.
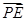 =λ
=λ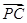 ,若DE∥平面PAB,求λ的值.
,若DE∥平面PAB,求λ的值.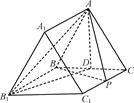
 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题:
是一条直线,以下命题: ,则
,则 ;②若
;②若 ,
, ,
,

 的侧棱
的侧棱 在下底面的射影
在下底面的射影 与
与 平行,若
平行,若 ,且
,且 ,则
,则 的余弦值为( )
的余弦值为( )



