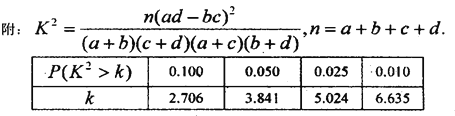题目内容
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

【答案】(I)![]() (II)见解析.
(II)见解析.
【解析】试题分析:
(1)利用等体积法结合题意可求得![]() 到平面
到平面![]() 的距离为
的距离为![]() ;
;
(2)当![]() 时满足题意,利用题中所给的条件进行证明即可.
时满足题意,利用题中所给的条件进行证明即可.
试题解析:
解:(1)方法一:因为![]() 平面
平面![]() ,
, ![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
方法二:等积法求高.
(2)解:在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 平面
平面![]() ,
,
下面给出证明:设![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() ,
,
过点![]() 作
作![]() 交于点
交于点![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运
会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.