题目内容
【题目】某早餐店每天制作甲、乙两种口味的糕点共n(nN*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理.该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下的统计数据:
甲口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 20 | 40 | 20 | 20 |
乙口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 40 | 30 | 20 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
【答案】(1)见解析;(2)![]() ,98.
,98.
【解析】试题分析:(1)由题意知![]() 的可能取值为
的可能取值为![]() 分别求出相应的概率,由此能求出
分别求出相应的概率,由此能求出![]() 分布列;(2)①求出
分布列;(2)①求出![]() ,由此能求出n的最大值; ②由(1)知在每天所制蛋糕能全部卖完时,
,由此能求出n的最大值; ②由(1)知在每天所制蛋糕能全部卖完时, ![]() ,此时销售这两种糕点的日总利润的期望值为
,此时销售这两种糕点的日总利润的期望值为![]() ,再求出当
,再求出当![]() 时,销售这两种糕点的日总利润的期望值,由此得到应选
时,销售这两种糕点的日总利润的期望值,由此得到应选![]() .
.
试题解析:(1)X所有可能的取值为96,97,98,99,100,101,102
P(X=96)=0.20.4=0.08
P(X=97)=0.20.3+0.40.4=0.22
P(X=98)= 0.20.2+0.40.3+0.20.4=0.24
P(X=99)= 0.20.1+0.40.2+0.20.3+0.20.4=0.24
P(X=100)= 0.40.1+0.20.2+0.20.3=0.14
P(X=101)= 0.20.1+0.20.2=0.06
P(X=102)= 0.20.1=0.02
X的分布列
X | 96 | 97 | 98 | 99 | 100 | 101 | 102 |
P | 0.08 | 0.22 | 0.24 | 0.24 | 0.14 | 0.06 | 0.02 |
(2)①依题意得,P(X<n)0.6,由P(X<99)=0.54,P(X<100)=0.78,n99
②记销售两种糕点的日总利润为Y,
当每天所制作糕点能全部卖完时,E(Y)96
当n=98时,E(Y)=(96-2)0.08+(97-1)0.22+980.7=97.24>96
选n=98

 能考试全能100分系列答案
能考试全能100分系列答案【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
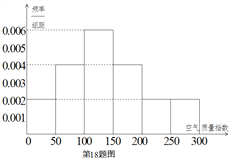
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.