题目内容
某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形, (
( 为圆柱的高,
为圆柱的高, 为球的半径,
为球的半径, ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
(1)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该储油罐的建造费用最小时的 的值.
的值.

 (
( 为圆柱的高,
为圆柱的高, 为球的半径,
为球的半径, ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.(1)写出
 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;(2)求该储油罐的建造费用最小时的
 的值.
的值.
(1)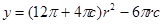 ,
,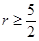 (2)
(2)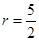 .
.
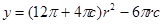 ,
,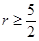 (2)
(2)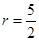 .
.试题分析:(1)求实际问题函数解析式,关键正确理解题意,列出正确的等量关系,明确自变量取值范围. 储油罐的建造费用等于圆柱形部分建造费用与半球形部分建造费用之和,
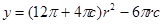 由
由 得:
得: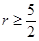 ,(2)所研究函数
,(2)所研究函数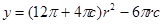 是一个关于
是一个关于 的一元二次函数,求其最值关键在于研究对称轴
的一元二次函数,求其最值关键在于研究对称轴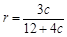 与定义区间
与定义区间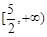 之间位置关系,
之间位置关系,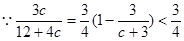
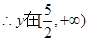 上是增函数,所以当
上是增函数,所以当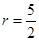 时,储油罐的建造费用最小.
时,储油罐的建造费用最小.[解] :(1)
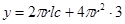 3分
3分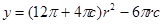 (
(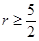 ) 6分
) 6分(2)
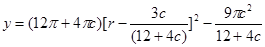 8分
8分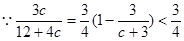
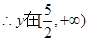 上是增函数 12分
上是增函数 12分所以当
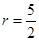 时,储油罐的建造费用最小. 14分
时,储油罐的建造费用最小. 14分
练习册系列答案
相关题目
 的定义域为
的定义域为 ,若函数
,若函数 ,使
,使 上的值域是
上的值域是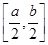 则称
则称 为“倍缩函数”,则的范围是( )
为“倍缩函数”,则的范围是( ) B.
B.
 D.
D.
 的取值范围是( )
的取值范围是( )




 是函数
是函数 的零点,
的零点,
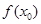 的值满足( )
的值满足( )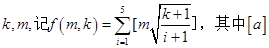 表示不大于a的最大整数,则
表示不大于a的最大整数,则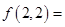 _________.
_________.