题目内容
类比“两角和与差的正弦公式”的形式,对于给定的两个函数:S(x)=ax-a-x,C(x)=
ax+a-x,其中a>0,且a≠1,下面正确的运算公式是( )
①S(x+y)=S(x)C(y)+C(x)S(y);
②S(x-y)=S(x)C(y)-C(x)S(y);
③2S(x+y)=S(x)C(y)+C(x)S(y);
④2S(x-y)=S(x)C(y)-C(x)S(y).
ax+a-x,其中a>0,且a≠1,下面正确的运算公式是( )
①S(x+y)=S(x)C(y)+C(x)S(y);
②S(x-y)=S(x)C(y)-C(x)S(y);
③2S(x+y)=S(x)C(y)+C(x)S(y);
④2S(x-y)=S(x)C(y)-C(x)S(y).
| A.①② | B.③④ | C.①④ | D.②③ |
B
经验证易知①②错误.依题意,注意到2S(x+y)=2(ax+y-a-x-y),又S(x)C(y)+C(x)S(y)=2(ax+y-a-x-y),因此有2S(x+y)=S(x)C(y)+C(x)S(y);同理有2S(x-y)=S(x)C(y)-C(x)S(y),综上所述,选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (
( 为圆柱的高,
为圆柱的高, 为球的半径,
为球的半径, ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
 .
. 为常数且
为常数且
 时,求
时,求 ;
; 满足
满足 ,但
,但 ,则称
,则称 的二阶周期点.证明函数
的二阶周期点.证明函数 ;
;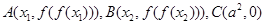 ,记
,记 的面积为
的面积为 ,求
,求 上的最大值和最小值。
上的最大值和最小值。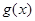 是R上的奇函数,且当
是R上的奇函数,且当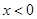 时,
时,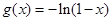 ,设函数
,设函数 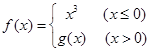 ,若
,若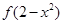
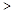
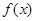 ,则实数
,则实数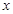 的取值范围是( )
的取值范围是( )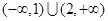


 内有零点,
内有零点, 内有零点,若m为整数,则m的值为 .
内有零点,若m为整数,则m的值为 . 上选择一点C建造垃圾处理厂,其对市区的影响度与所选地
上选择一点C建造垃圾处理厂,其对市区的影响度与所选地  的两个极值点,且
的两个极值点,且 则b的最大值为_________.
则b的最大值为_________. 满足
满足 ,当x∈[0,1]时,
,当x∈[0,1]时, ,若在区间(-1,1]上,
,若在区间(-1,1]上, 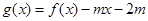 有两个零点,则实数m的取值范围是
有两个零点,则实数m的取值范围是