题目内容
(5分)(2011•福建)在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k丨n∈Z},k=0,1,2,3,4.给出如下四个结论:
①2011∈[1];
②﹣3∈[3];
③Z=[0]∪[1]∪[2]∪[3]∪[4];
④“整数a,b属于同一“类”的充要条件是“a﹣b∈[0]”.
其中,正确结论的个数是( )
①2011∈[1];
②﹣3∈[3];
③Z=[0]∪[1]∪[2]∪[3]∪[4];
④“整数a,b属于同一“类”的充要条件是“a﹣b∈[0]”.
其中,正确结论的个数是( )
| A.1 | B.2 | C.3 | D.4 |
C
试题分析:根据题中“类”的理解,在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,
对于各个结论进行分析:①∵2011÷5=402…1;②∵﹣3÷5=0…2,③整数集中的数被5除的数可以且只可以分成五类,故Z=[0]∪[1]∪[2]∪[3]∪[4];④从正反两个方面考虑即可.
解:①∵2011÷5=402…1,∴2011∈[1],故①对;
②∵﹣3=5×(﹣1)+2,∴对﹣3∉[3];故②错;
③∵整数集中的数被5除的数可以且只可以分成五类,故Z=[0]∪[1]∪[2]∪[3]∪[4],故③对;
④∵整数a,b属于同一“类”,∴整数a,b被5除的余数相同,从而a﹣b被5除的余数为0,反之也成立,故“整数a,b属于同一“类”的充要条件是“a﹣b∈[0]”.故④对.
∴正确结论的个数是3.
故选C.
点评:本题主要考查了选修3同余的性质,具有一定的创新,关键是对题中“类”的题解,属于创新题.

练习册系列答案
相关题目
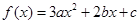 ,且有
,且有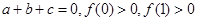 .
.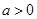 ,且
,且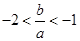 ;
;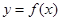 在区间
在区间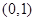 内有两个不同的零点.
内有两个不同的零点. (
( 为圆柱的高,
为圆柱的高, 为球的半径,
为球的半径, ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
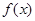 满足对任意的
满足对任意的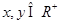 恒有
恒有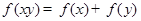 ,且当
,且当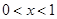 时,
时,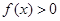 .
.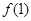 的值;
的值;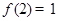 ,解不等式
,解不等式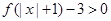 .
.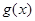 是R上的奇函数,且当
是R上的奇函数,且当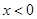 时,
时,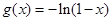 ,设函数
,设函数 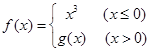 ,若
,若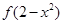
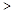
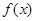 ,则实数
,则实数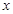 的取值范围是( )
的取值范围是( )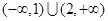


 (A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是________.
(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是________. 内有零点,
内有零点, 内有零点,若m为整数,则m的值为 .
内有零点,若m为整数,则m的值为 . 的两个极值点,且
的两个极值点,且 则b的最大值为_________.
则b的最大值为_________.