题目内容
【题目】长方形![]() 中,
中,![]() ,
,![]() 是
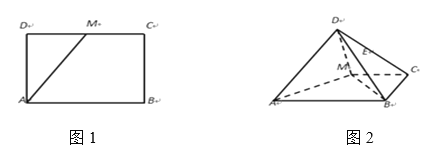
是![]() 中点(图1).将
中点(图1).将![]() 沿
沿![]() 折起,使得
折起,使得![]() (图2)在图2中:
(图2)在图2中:
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存点
上是否存点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,说明理由.
,说明理由.
【答案】(1)证明见解析(2)存在,理由见解析
【解析】
(1)利用勾股定理与线面垂直的性质证明![]() 平面
平面![]() 即可.
即可.
(2) 以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系. 设
轴,建立空间直角坐标系. 设![]() ,再根据二面角的向量方法,分别求解面的法向量,再根据法向量的夹角求解即可.
,再根据二面角的向量方法,分别求解面的法向量,再根据法向量的夹角求解即可.
(1)在长方形![]() 中,连结
中,连结![]() ,因为
,因为![]() ,
,![]() 是
是![]() 中点,
中点,
所以![]() ,从而
,从而![]() ,
,
所以![]()
因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)因为平面![]() 平面
平面![]() ,交线是
,交线是![]() ,
,
所以在面![]() 过
过![]() 垂直于
垂直于![]() 的直线必然垂直平面
的直线必然垂直平面![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,
轴,
建立空间直角坐标系.
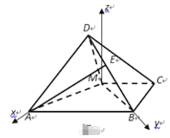
则![]() ,
,![]() ,
,![]() ,
,![]() .设
.设![]() ,则
,则![]() .
.
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则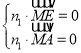 ,即
,即![]() ,取
,取![]() ,
,
平取面![]() 的一个法向量是
的一个法向量是![]() .
.
依题意![]() ,
,
即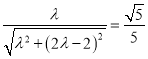 ,解方程得
,解方程得![]() ,
,
因此在线段![]() 上存点
上存点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】工厂抽取了在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
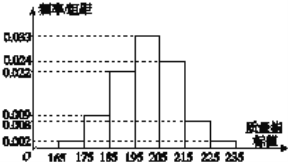
(1)计算该样本的平均值![]() ,方差
,方差![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(2)若质量指标值在![]() 之内为一等品.
之内为一等品.
(i)用样本估计总体,问该工厂一天生产的产品是否有![]() 以上为一等品?
以上为一等品?
(ii)某天早上、下午分别抽检了50件产品,完成下面的表格,并根据已有数据,判断是否有![]() 的把握认为一等品率与生产时间有关?
的把握认为一等品率与生产时间有关?
一等品个数 | 非一等品个数 | 总计 | |
早上 | 36 | 50 | |
下午 | 26 | 50 | |
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.010 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
参考数据:![]() .
.
【题目】随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄 (单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.