Question

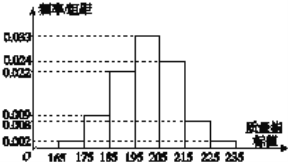
【题目】工厂抽取了在一段时间内生产的一批产品，测量一项质量指标值，绘制了如图所示的频率分布直方图.

（1）计算该样本的平均值，方差；（同一组中的数据用该组区间的中点值作代表）

（2）若质量指标值在之内为一等品.

（i）用样本估计总体，问该工厂一天生产的产品是否有以上为一等品？

（ii）某天早上、下午分别抽检了50件产品，完成下面的表格，并根据已有数据，判断是否有的把握认为一等品率与生产时间有关？

	一等品个数	非一等品个数	总计
早上	36		50
下午	26		50
总计

附：.

	0.25	0.15	0.10	0.050	0.010	0.001
	1.323	2.072	2.706	3.841	6.635	10.828

参考数据：.

Answer 1

【答案】（1），；（2）（i）有以上为一等品；（ii）详见解析.

【解析】

（1）区间中点值和频率的乘积，再分别相加可得平均数，再利用方差公式可求方差；

（2）（i）由质量指标值在之间的频率可得一等品的百分比；

（ii）根据列联表和卡方公式，求出卡方值，再进行判断.

解：（1）由频率分布直方图可得

，

.

（2）（i）由（1）得，

由图可得质量指标值在之间的频率为，

所以有以上为一等品.

（ii）补全的表格如下.

	一等品个数	非一等品个数	总计
早上	36	14	50
下午	26	24	50
总计	62	38	100

由此得，

所以有的把握认为一等品率与生产时间有关.