题目内容
【题目】已知函数f(x)的定义域[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示
x | ﹣1 | 0 | 2 | 4 | 5 |
F(x) | 1 | 2 | 1.5 | 2 | 1 |
下列关于函数f(x)的命题;
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数
③如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)﹣a最多有4个零点.
其中正确命题的序号是 . 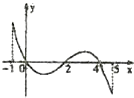
【答案】①②④
【解析】解:由f(x)的导函数y=f′(x)的图象可看出:如表格,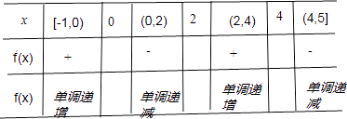
由表格可知:函数f(x)在区间[﹣1,0)上单调递增,在区间(0,2)上单调递减,在区间(2,4)上单调递增,在区间(4,5]上单调递增.∴②正确.
∴函数f(x)在x=0和x=4时,分别取得极大值,在x=2时取得极小值,且由对应值表f(0)=2,f(2)=1.5,
f(4)=2,又f(﹣1)=1,f(5)=1.
∴函数f(x)的值域为[1,2].∴①正确.
根据已知的对应值表及表格画出图象如下图: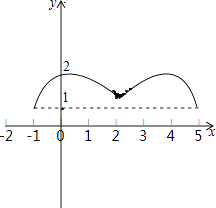
③根据以上知识可得:当x∈[﹣1,t]时,f(x)的最大值是2,则t=0,或4.故③不正确.
④由图象可以看出:当1.5<a<2时,函数y=f(x)﹣a有4个零点;当a=2时,函数y=f(x)﹣a有2个
3零点;当a=1.5时,函数y=f(x)﹣a有3个零点;当1≤a<1.5时,函数y=f(x)﹣a有4个零点;
∴当1<a<2时,函数y=f(x)﹣a最多有4个零点.故④正确.
综上可知①②④正确.
所以答案是①②④.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目