题目内容
【题目】已知函数f(x)=xlnx
(1)求f(x)在点(1,f(1))处的切线方程;
(2)若函数 ![]() 在[1,e]上的最小值为
在[1,e]上的最小值为 ![]() ,求a的值;
,求a的值;
(3)若k∈Z,且f(x)+x﹣k(x﹣1)>0对任意x>1恒成立,求k的最大值.
【答案】
(1)解:∵f(x)=xlnx∴f′(x)=lnx+1
∴f′(1)=1,f(1)=0
则切线方程为y﹣0=1(x﹣1),即y=x﹣1
(2)解:F(x)=lnx﹣ ![]() ,F′(x)=
,F′(x)= ![]() ,
,
①当a≥0时,F′(x)>0,F(x)在[1,e]上单调递增,F(x)在[1,e]上的最小值为F(1)=﹣a= ![]() ,解得a=﹣
,解得a=﹣ ![]() (0,+∞),故舍去.
(0,+∞),故舍去.
②当a∈(﹣1,0)时,F(x)在[1,e]上单调递增,F(x)在[1,e]上的最小值为F(1)=﹣a= ![]() ,解得a=﹣
,解得a=﹣ ![]() (﹣1,0),故舍去
(﹣1,0),故舍去
③当a∈[﹣e,﹣1]时,F(x)在[1,﹣a]上单调递减,F(x)在[﹣a,e]上递增,F(x)在[1,e]上的最小值为F(﹣a)=ln(﹣a)+1= ![]()
解得a=﹣ ![]() ∈[﹣e,﹣1],故符合题意.
∈[﹣e,﹣1],故符合题意.
④当a∈(﹣∞,﹣e)时,F(x)在[1,e]上单调递减,F(x)在[1,e]上的最小值为F(e)=1﹣ ![]() =
= ![]() ,解得a=﹣
,解得a=﹣ ![]() (﹣∞,﹣e),故舍去
(﹣∞,﹣e),故舍去
综上:a=﹣ ![]()
(3)解:令g(x)=f(x)+x﹣k(x﹣1)=xlnx+x﹣k(x﹣1)(x>1)g'(x)=lnx+2﹣k(x>1)
①当k≤2时,g'(x)>0在(1,+∞)上恒成立,g(x)在(1,+∞)上恒成立,g(x)min=g(1)=1>0
②当k>2时,令g'(x)=0得x=ek﹣2
当x变化时,g'(x)、g(x)变化情况如下表:
x | (1,ek﹣2) | ek﹣2 | (ek﹣2,+∞) |
g′(x) | ﹣ | 0 | + |
g(x) | 减函数 | 极小值 | 增函数 |
∴ ![]() 即ek﹣2(k﹣2)+ek﹣2﹣k(ek﹣2﹣1)>0
即ek﹣2(k﹣2)+ek﹣2﹣k(ek﹣2﹣1)>0
即k>ek﹣2,∴lnk>k﹣2,∴lnk﹣k+2>0,
令h(k)=lnk﹣k+2,(k>0).
h′(k)= ![]() ,当k∈(0,1)时,h(k)递增,k∈(1,+∞)递减,
,当k∈(0,1)时,h(k)递增,k∈(1,+∞)递减,
且h(1)=1>0,h(2)=ln2>0,h(3)=ln3﹣1>0,h(4)=ln4﹣2<,0∴3<k<4
∴整数k的最大值是3
【解析】(1)由f′(x)=lnx+1,得f′(1)=1,由f(1)=0得切点,即可得切线方程.(2)F(x)=lnx﹣ ![]() ,F′(x)=
,F′(x)= ![]() ,分①当a≥0,②当a∈(﹣1,0),③当a∈[﹣e,﹣1],④当a∈(﹣∞,﹣e) 求出F(x)的最小值,由最小值为
,分①当a≥0,②当a∈(﹣1,0),③当a∈[﹣e,﹣1],④当a∈(﹣∞,﹣e) 求出F(x)的最小值,由最小值为 ![]() ,求解a.(3)令g(x)=f(x)+x﹣k(x﹣1)=xlnx+x﹣k(x﹣1)(x>1),分 ①当k≤2,②当k>2时,求出g(x)的最小值,最小值大于0即可求解k的最大值.
,求解a.(3)令g(x)=f(x)+x﹣k(x﹣1)=xlnx+x﹣k(x﹣1)(x>1),分 ①当k≤2,②当k>2时,求出g(x)的最小值,最小值大于0即可求解k的最大值.
【考点精析】根据题目的已知条件,利用函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

 津桥教育计算小状元系列答案
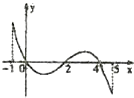
津桥教育计算小状元系列答案【题目】已知函数f(x)的定义域[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示
x | ﹣1 | 0 | 2 | 4 | 5 |
F(x) | 1 | 2 | 1.5 | 2 | 1 |
下列关于函数f(x)的命题;
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数
③如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)﹣a最多有4个零点.
其中正确命题的序号是 .