题目内容
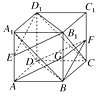
【题目】如图所示，已知正方体ABCD－A1B1C1D1.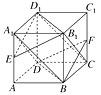
（1）求证：平面A1BD∥平面B1D1C.
（2）若E ， F分别是AA1 ， CC1的中点，求证：平面EB1D1∥平面FBD.
【答案】
（1）证明：因为 
，所以四边形BB1D1D是平行四边形，
所以B1D1∥BD，又BD平面B1D1C，B1D1平面B1D1C，所以BD∥平面B1D1C.
同理A1D∥平面B1D1C，又A1D∩BD＝D，所以平面A1BD∥平面B1D1C.
（2）证明：由BD∥B1D1，得BD∥平面EB1D1，取BB1的中点G，连接AG，GF，易得AE∥B1G，
又因为AE＝B1G，所以四边形AEB1G是平行四边形，所以B1E∥AG.易得GF∥AD.
又因为GF＝AD，所以四边形ADFG是平行四边形，所以AG∥DF，所以B1E∥DF，
DF平面EB1D1，B1E平面EB1D1，所以DF∥平面EB1D1.
又因为BD∩DF＝D，所以平面EB1D1∥平面FBD
【解析】本题要证明面面平行，根据平面与平面平行的判定及平面与平面平行的性质进行判断。基本思路为;由线线平行
线面平行面面平行。重要是把题目读懂把已知条件充分利用起来，没得关联就找辅助线。
练习册系列答案
相关题目
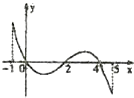
【题目】已知函数f（x）的定义域[﹣1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示
x | ﹣1 | 0 | 2 | 4 | 5 |
F（x） | 1 | 2 | 1.5 | 2 | 1 |
下列关于函数f（x）的命题；
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数
③如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）﹣a最多有4个零点．
其中正确命题的序号是 ． 
