题目内容
【题目】若不等式ax2﹣bx+c>0的解集为{x|﹣2<x<3},求不等式cx2﹣bx﹣a<0的解集.
【答案】解:根据题意,若不等式ax2﹣bx+c>0的解集为{x|﹣2<x<3},
则﹣2,3是对应方程ax2+bx+c=0的两个根,且a<0,
则有 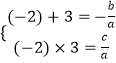 ,解可得b=﹣a,c=﹣6a,
,解可得b=﹣a,c=﹣6a,
则不等式cx2+bx+a>0等价为﹣6ax2﹣ax+a>0,
又由a<0,
则有6x2+x﹣1>0,
即(2x+1)(3x﹣1)>0,
解可得x> ![]() 或x<﹣
或x<﹣ ![]() ,
,
故不等式cx2﹣bx﹣a<0的解集为{x|x> ![]() 或x<﹣
或x<﹣ ![]() }.
}.
【解析】根据不等式的解集与一元二次方程根的情况,利用韦达定理可求出b=﹣a,c=﹣6a,得到新的不等式,因为a<0所以得到6x2+x﹣1>0,解得即可。
【考点精析】解答此题的关键在于理解解一元二次不等式的相关知识,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知函数f(x)的定义域[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示
x | ﹣1 | 0 | 2 | 4 | 5 |
F(x) | 1 | 2 | 1.5 | 2 | 1 |
下列关于函数f(x)的命题;
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数
③如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)﹣a最多有4个零点.
其中正确命题的序号是 .