Question

15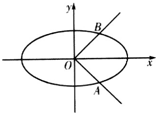．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{6}}}{3}$，点O为坐标原点，椭圆C与曲线|y|=x的交点分别为A，B（A在第四象限），且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）定义：以原点O为圆心，$\sqrt{{a^2}+{b^2}}$为半径的圆称为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的“伴随圆”．若直线l交椭圆C于M，N两点，交其“伴随圆”于P，Q两点，且以MN为直径的圆过原点O．
证明：|PQ|为定值．

Answer 1

分析 （Ⅰ）因为$c=\frac{\sqrt{6}}{3}$，所以$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{2}{3}$，得$\frac{{b}^{2}}{{a}^{2}}=\frac{1}{3}$，即可求得椭圆方程．
（Ⅱ）由“半椭圆”的方程与直线联立，由$\overrightarrow{OM}•\overrightarrow{ON}=0$得x₁x₂+y₁y₂=0，代入即可解得．

解答 解：（Ⅰ）因为$c=\frac{\sqrt{6}}{3}$，所以$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{2}{3}$，得$\frac{{b}^{2}}{{a}^{2}}=\frac{1}{3}$
联立$\left\{\begin{array}{l}{y=x}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$得${x}^{2}=\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$，$x=±\frac{\sqrt{3}}{2}b$，故A（$\frac{\sqrt{3}}{2}b，-\frac{\sqrt{3}}{2}b$），B（$\frac{\sqrt{3}}{2}b，\frac{\sqrt{3}}{2}b$）
由$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$得（$\frac{\sqrt{3}}{2}b，\frac{\sqrt{3}}{2}b$）$•（0，\sqrt{3}b）=\frac{3}{2}$，解得b²=1，a²=3
所以椭圆方程为$\frac{{x}^{2}}{3}+{y}^{2}=1$
（Ⅱ）由题意可得“半椭圆”方程x²+y²=4
当直线l斜率不存在时，设l：x=n，代入椭圆方程得M（n，$\sqrt{1-\frac{{n}^{2}}{3}}$），N（n，-$\sqrt{1-\frac{{n}^{2}}{3}}$）
由$\overrightarrow{OM}•\overrightarrow{ON}=0$，得$n=±\frac{\sqrt{3}}{2}$，代入x²+y²=4得y=$±\frac{\sqrt{13}}{2}$，所以|PQ|=$\sqrt{13}$．
当直线l斜率存在时，设l为方程为y=kx+m（k，m∈R）且与椭圆得交点M（x₁，y₁）N（x₂，y₂）
联立方程组$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$整理得（1+3k²）x²+6kmx+3m²-3=0
△=36k²m²-4（1+3k²）（3m²-3）＞0，即m²＜3k²+1
∵x₁+x₂=$\frac{-6km}{1+3{k}^{2}}，{x}_{1}{x}_{2}=\frac{3{m}^{2}-3}{1+3{k}^{2}}$
可得y₁y₂=（kx₁+m）（kx₂+m）=$\frac{{m}^{2}-3{k}^{2}}{1+3{k}^{2}}$
由$\overrightarrow{OM}•\overrightarrow{ON}=0$得x₁x₂+y₁y₂=0，即$\frac{3{m}^{2}-3}{1+3{k}^{2}}+\frac{{m}^{2}-3{k}^{2}}{1+3{k}^{2}}=\frac{4{m}^{2}-3{k}^{2}-3}{1+3{k}^{2}}=0$
所以${m}^{2}=\frac{3}{4}（{k}^{2}+1）$，代入验证△＞0，
即原点O到直线l的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}=\sqrt{\frac{{m}^{2}}{1+{k}^{2}}=\frac{\sqrt{3}}{2}}$
∵“半椭圆”的半径为2，∴$|PQ|=2\sqrt{4-\frac{3}{4}}=\sqrt{13}$
综上，|PQ|为定值$\sqrt{13}$

点评 本题主要考查了圆锥曲线的方程求法和新定义下的圆锥曲线与直线综合题的应用，属于中档题型．