题目内容
下列四个函数:①y=3-x;②y=
;③y=x2+2x-10;④y=
,其中值域为R的函数有( )
| 1 |
| x2+1 |
|
| A.1个 | B.2个 | C.3个 | D.4个 |
根据一次函数的值域为R,y=3-x为一次函数,故①满足条件;
根据x2+1≥1,可得0<
≤1,即函数y=
的值域为(0,1],故②不满足条件;
二次函数y=x2+2x-10的最小值为-11,无最大值,故函数y=x2+2x-10的值域为[-11,+∞),故③不满足条件;
当x≤0时,y=-x≥0,当x>0时,y=-
<0,故函数y=
的值域为R,故④满足条件;
故选B
根据x2+1≥1,可得0<
| 1 |
| x2+1 |
| 1 |
| x2+1 |
二次函数y=x2+2x-10的最小值为-11,无最大值,故函数y=x2+2x-10的值域为[-11,+∞),故③不满足条件;
当x≤0时,y=-x≥0,当x>0时,y=-
| 1 |
| x |
|
故选B

练习册系列答案
相关题目
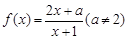 .
. 不可能为偶函数;
不可能为偶函数;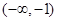 上单调递减的充要条件是
上单调递减的充要条件是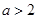 .
.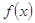 在
在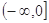 上单调递减,则不等式
上单调递减,则不等式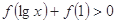 的解集是 .
的解集是 . 在区间
在区间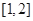 上的最小值是( )
上的最小值是( )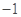
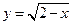 的定义域为
的定义域为