题目内容
3.已知函数f(x)=ex(sinx+a)在R上单调递增,则实数a的取值范围是$a≥\sqrt{2}$.分析 求函数的导数,要使函数单调递增,则f′(x)≥0立,然后求出实数a的取值范围.
解答 解:因为f(x)=ex(sinx+a),所以f′(x)=ex(sinx+a+cosx).
要使函数单调递增,则f′(x)≥0成立.
即sinx+a+cosx≥0恒成立.
所以a≥-sinx-cosx,
因为-sinx-cosx=-$\sqrt{2}$sin(x+$\frac{π}{4}$)
所以-$\sqrt{2}$≤-sinx-cosx≤$\sqrt{2}$,
所以$a≥\sqrt{2}$,
故答案为:$a≥\sqrt{2}$.
点评 本题主要考查导数的基本运算以及利用导数研究函数的单调性,注意当函数单调递增时,f'(x)≥0恒成立.

练习册系列答案
相关题目
13.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是减函数,若$f({ln\frac{n}{m}})-f(1)>0$,则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是( )
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
18.已知函数f(x)=$\left\{\begin{array}{l}3,x≥m\\{x}^{2}+5x-12,x<m\end{array}\right.$,若函数g(x)=f(x)-x恰有三个不同的零点,则实数m的取值范围是( )
| A. | m<2 | B. | 2<m≤3 | C. | 2≤m≤3 | D. | m>3 |
15.已知a,b是实数,则“a>|b|”是“a2>b2”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
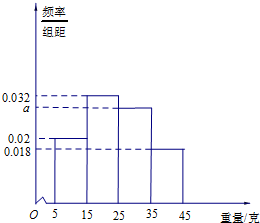 测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.
测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.