题目内容
已知函数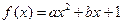 (
(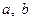 为实数,
为实数,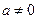 ,
,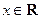 ),
),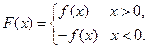
(1)若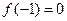 ,且函数
,且函数 的值域为
的值域为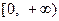 ,求
,求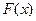 的表达式;
的表达式;
(2)在(1)的条件下,当 时,
时,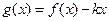 是单调函数,求实数
是单调函数,求实数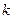 的取值范围;
的取值范围;
(3)设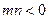 ,
,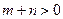 ,
,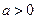 ,且函数
,且函数 为偶函数,判断
为偶函数,判断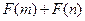 是否大于
是否大于 ?
?
解:(Ⅰ)因为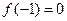 ,所以
,所以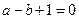 .
.
因为 的值域为
的值域为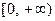 ,所以
,所以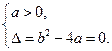 ……… 2分
……… 2分
所以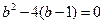 .解得
.解得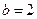 ,
,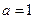 .所以
.所以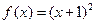 .
.
所以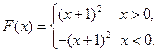 ………… 4分
………… 4分
(Ⅱ)因为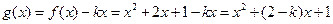
=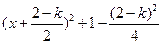 , ……… 6分
, ……… 6分
所以当 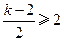 或
或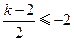 时
时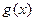 单调.
单调.
即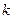 的范围是
的范围是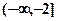 或
或 时,
时,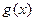 是单调函数. … 8分
是单调函数. … 8分
(Ⅲ)因为 为偶函数,所以
为偶函数,所以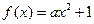 .
.
所以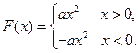 …………… 10分
…………… 10分
因为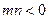 , 依条件设
, 依条件设 ,则
,则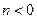 .
.
又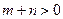 ,所以
,所以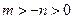 .
.
所以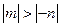 . ……………… 12分
. ……………… 12分
此时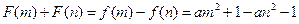
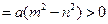 .
.
即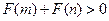 .
.
解析

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
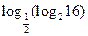 ;
;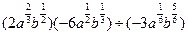 .
.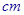 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积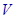 与
与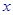 的函数关系式,并求出函数的定义域.
的函数关系式,并求出函数的定义域.  能源产品,估计能获得x∈[10,1000]万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
能源产品,估计能获得x∈[10,1000]万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.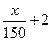 ;(ii) y=4lgx-3.试分析这两个函数模型
;(ii) y=4lgx-3.试分析这两个函数模型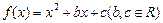 ,已知不论
,已知不论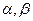 为何实数恒有
为何实数恒有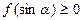 ,
,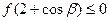
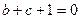 ;
; 2)求证:
2)求证: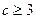 ;
;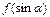 的最大值为8,求
的最大值为8,求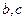 值.
值.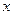 满足不等式
满足不等式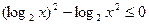 ,求函数
,求函数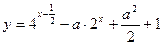 的最小值.
的最小值. 维护费50元.
维护费50元. 少?
少? 分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率
分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率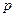 与每日生产产品件数
与每日生产产品件数 (
(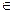
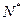 )间的关系为
)间的关系为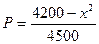 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)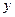 (元)表示成日产量
(元)表示成日产量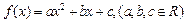 满足:对任意实数x,都有
满足:对任意实数x,都有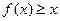 ,且当
,且当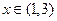 时,有
时,有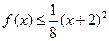 成立.
成立. 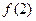 ;
; 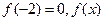 的表达式;
的表达式;  ,若
,若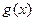 图上的点都位于直线
图上的点都位于直线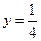 的上方,求实
的上方,求实