题目内容
(本题满分14分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要 维护费50元.
维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多 少?
少?
解:(1)当每辆车的月租金定为3600元时,未租出的车辆数为: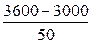 =12,所以这时租出了88辆车………………………………………………………………………..…4分
=12,所以这时租出了88辆车………………………………………………………………………..…4分
(2)设每辆车的月租金定为x元,则租赁公司的月收益为:
f( x)=(100-
x)=(100-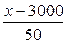 )(x-150)-
)(x-150)-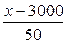 ×50,…………….…….……....10分
×50,…………….…….……....10分
整理得f(x)=-
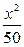 +162x-21000=-
+162x-21000=-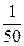 (x-4050)2+307050……………………...12分
(x-4050)2+307050……………………...12分
所以,当x=4050时,f(x)最大,其最大值为f(4050)=307050.
即当每辆车月租金定为4050元时,租赁公司月收益最大,最大收益为307050元.………..14分
解析

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
曲线f(x)=x3+x﹣2在p0处的切线平行于直线y=4x﹣1,则p0的坐标为( )
| A.(1,0) | B.(2,8) |
| C.(1,0)或(﹣1,﹣4) | D.(2,8)或(﹣1,﹣4) |
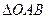 是边长为2的正三角形,记
是边长为2的正三角形,记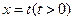 左侧的图形的面积为
左侧的图形的面积为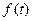 ,试求函数
,试求函数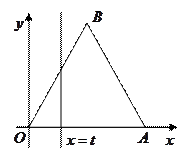
 某种商品的经验表明,该商品每日的销售量
某种商品的经验表明,该商品每日的销售量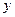 (单位:千克)与销售价格
(单位:千克)与销售价格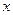 (单位:元/千克)满
(单位:元/千克)满 足关系式
足关系式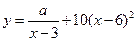 ,其中
,其中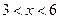 ,
,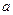 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克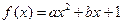 (
(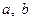 为实数,
为实数,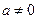 ,
,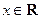 ),
),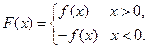
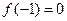 ,且函数
,且函数 的值域为
的值域为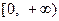 ,求
,求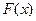 的表达式;
的表达式; 时,
时,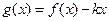 是单调函数,求实数
是单调函数,求实数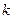 的取值范围;
的取值范围;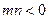 ,
,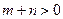 ,
,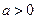 ,且函数
,且函数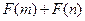 是否大于
是否大于 ?
?
 的图像经过坐
的图像经过坐 标原
标原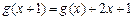 ,设函数
,设函数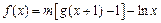 ,其中m为常数且
,其中m为常数且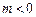 。
。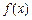 的单调性并说明理由。
的单调性并说明理由。 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0). 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;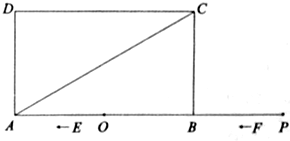
 的图象与x轴有两个不同的公共点,且
的图象与x轴有两个不同的公共点,且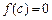 ,当
,当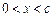 时,恒有
时,恒有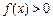 .
.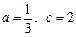 时,求不等式
时,求不等式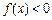 的解集;
的解集;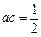 ,求a的值;
,求a的值;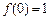 ,且
,且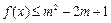 对所有
对所有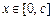 恒成立,求正实数m的最小值.
恒成立,求正实数m的最小值.