题目内容
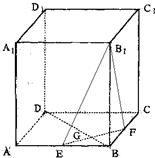
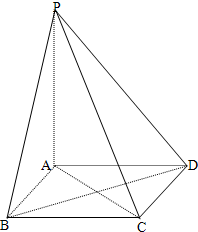
如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2
,侧棱长为4,E、F分别是棱AB,BC的中点,EF与BD相交于G.
(1)求证:平面EFB1⊥平面BDD1B1;
(2)求点B到平面B1EF的距离.
| 2 |
(1)求证:平面EFB1⊥平面BDD1B1;
(2)求点B到平面B1EF的距离.

(1)证明:∵EF∥AC,AC⊥BD,∴EF⊥BD,根据正四棱柱的性质EF⊥BB1,BD∩BB1=B,可知EF⊥平面BDD1B1,…(3分)
又EF?面B1EF,∴面EFB1⊥面BDD1B1…(7分)
(2)可知∴面EFB1⊥面BDD1B1,在平面BDD1B1中,作BH⊥B1G于为H,∵面EFB1⊥面BDD1B1,面EFB1∩面BDD1B1=B1G
∴BH⊥面B1EF,BH就是点B到平面B1EF的距离…(10分)
在Rt△B1BG中,B1B=4,BG=1,BH⊥B1G⇒BH=
=
…(12分)
又EF?面B1EF,∴面EFB1⊥面BDD1B1…(7分)
(2)可知∴面EFB1⊥面BDD1B1,在平面BDD1B1中,作BH⊥B1G于为H,∵面EFB1⊥面BDD1B1,面EFB1∩面BDD1B1=B1G
∴BH⊥面B1EF,BH就是点B到平面B1EF的距离…(10分)
在Rt△B1BG中,B1B=4,BG=1,BH⊥B1G⇒BH=
| BG•BB1 |
| B1G |
4
| ||
| 17 |

练习册系列答案
相关题目

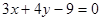 和
和 的距离是_______.
的距离是_______.