题目内容
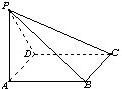
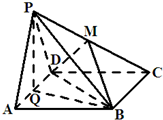
ABCD为平行四边形,P为平面ABCD外一点,PA⊥面ABCD,且PA=AD=2,AB=1,AC=
.
(1)求证:平面ACD⊥平面PAC;
(2)求异面直线PC与BD所成角的余弦值;
(3)设二面角A-PC-B的大小为θ,试求tanθ的值.
| 3 |
(1)求证:平面ACD⊥平面PAC;
(2)求异面直线PC与BD所成角的余弦值;
(3)设二面角A-PC-B的大小为θ,试求tanθ的值.

证明:(1)∵PA⊥面ABCD,
PA?平面PAC
∴平面ACD⊥平面PAC;
(2)令AC与BD交点为O,PA的中点为E,连接OE,BE如图所示:
∵O为BD的中点,则EO=
PC=
=
,且OE∥PC
又∵PA⊥面ABCD,且PA=AD=2,AB=1,AC=
.
∴OB=
BD=
,BE=
∴|cos∠EOB|=|
|=
;
即异面直线PC与BD所成角的余弦值为
;
(3)过A作AE⊥PC交PC于E,过E作EF⊥PC交PB于F,连接AE.则二面角A-PC-B的平面角为∠AEF即∠AEF=θ.
在Rt△APC中,PC=
,∴AE=
=
,PE=
=
,
在△PBC中,PB=
,BC=2,∴cos∠BPC=
=
,
在Rt△PEF中,tan∠EPF=
,∴EF=PE•tan∠EPF=
在△PAF中,PF=
=
,cos∠FPA=
=
,∴AF=1,
在△AEF中,cosθ=
,∴tanθ=
PA?平面PAC
∴平面ACD⊥平面PAC;
(2)令AC与BD交点为O,PA的中点为E,连接OE,BE如图所示:

∵O为BD的中点,则EO=
| 1 |
| 2 |
| 1 |
| 2 |
| PA2+AC2 |
| ||
| 2 |
又∵PA⊥面ABCD,且PA=AD=2,AB=1,AC=
| 3 |
∴OB=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
∴|cos∠EOB|=|
| OE2+OB2-BE2 |
| 2OE•OB |
| 3 |
| 7 |
即异面直线PC与BD所成角的余弦值为
| 3 |
| 7 |
(3)过A作AE⊥PC交PC于E,过E作EF⊥PC交PB于F,连接AE.则二面角A-PC-B的平面角为∠AEF即∠AEF=θ.
在Rt△APC中,PC=
| 7 |
| AP•AC |
| PC |
2
| ||
|
| PA2-AE2 |
| 4 | ||
|
在△PBC中,PB=
| 5 |
| PC2+PB2-BC2 |
| 2PC•PB |
| 4 | ||
|
在Rt△PEF中,tan∠EPF=
| ||
| 4 |
| ||
|
在△PAF中,PF=
| PE2+EF2 |
| 5 |
| PA |
| PB |
| 2 | ||
|
在△AEF中,cosθ=
2
| ||
|
| ||
| 6 |

练习册系列答案
相关题目