题目内容
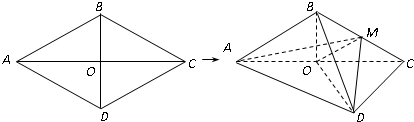
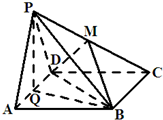
如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3
.
(Ⅰ)求证:OM∥平面ABD;
(Ⅱ)求证:平面ABC⊥平面MDO;
(Ⅲ)求三棱锥M-ABD的体积.
| 2 |
(Ⅰ)求证:OM∥平面ABD;
(Ⅱ)求证:平面ABC⊥平面MDO;
(Ⅲ)求三棱锥M-ABD的体积.

(Ⅰ)证明:因为点O是菱形ABCD的对角线的交点,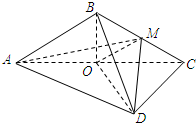
所以O是AC的中点.又点M是棱BC的中点,
所以OM是△ABC的中位线,OM∥AB.…(2分)
因为OM?平面ABD,AB?平面ABD,
所以OM∥平面ABD.…(4分)
(Ⅱ)证明:由题意,OM=OD=3,
因为DM=3
,所以∠DOM=90°,OD⊥OM.…(6分)
又因为菱形ABCD,所以OD⊥AC.…(7分)
因为OM∩AC=O,
所以OD⊥平面ABC,…(8分)
因为OD?平面MDO,
所以平面ABC⊥平面MDO.…(9分)
(Ⅲ)三棱锥M-ABD的体积等于三棱锥D-ABM的体积.…(10分)
由(Ⅱ)知,OD⊥平面ABC,
所以OD=3为三棱锥D-ABM的高.…(11分)
△ABM的面积为
BA×BM×sin120°=
×6×3×
=
,…(12分)
所求体积等于
×S△ABM×OD=
.…(13分)

所以O是AC的中点.又点M是棱BC的中点,
所以OM是△ABC的中位线,OM∥AB.…(2分)
因为OM?平面ABD,AB?平面ABD,
所以OM∥平面ABD.…(4分)
(Ⅱ)证明:由题意,OM=OD=3,
因为DM=3
| 2 |
又因为菱形ABCD,所以OD⊥AC.…(7分)
因为OM∩AC=O,
所以OD⊥平面ABC,…(8分)
因为OD?平面MDO,
所以平面ABC⊥平面MDO.…(9分)
(Ⅲ)三棱锥M-ABD的体积等于三棱锥D-ABM的体积.…(10分)
由(Ⅱ)知,OD⊥平面ABC,
所以OD=3为三棱锥D-ABM的高.…(11分)
△ABM的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
9
| ||
| 2 |
所求体积等于
| 1 |
| 3 |
9
| ||
| 2 |

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
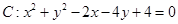 的圆心到直线
的圆心到直线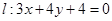 的距离
的距离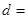 .
.