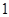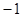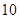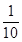题目内容
定义在R上的函数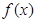 ,其图象是连续不断的,如果存在非零常数
,其图象是连续不断的,如果存在非零常数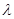 (
(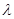 ∈R,使得对任意的x
∈R,使得对任意的x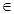 R,都有f(x+
R,都有f(x+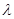 )=
)=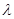 f(x),则称y=f(x)为“倍增函数”,
f(x),则称y=f(x)为“倍增函数”,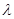 为“倍增系数”,下列命题为真命题的是____(写出所有真命题对应的序号).
为“倍增系数”,下列命题为真命题的是____(写出所有真命题对应的序号).
①若函数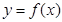 是倍增系数
是倍增系数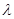 =-2的倍增函数,则
=-2的倍增函数,则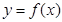 至少有1个零点;
至少有1个零点;
②函数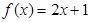 是倍增函数,且倍增系数
是倍增函数,且倍增系数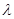 =1;
=1;
③函数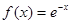 是倍增函数,且倍增系数
是倍增函数,且倍增系数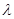 ∈(0,1);
∈(0,1);
④若函数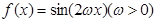 是倍增函数,则
是倍增函数,则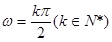
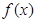 ,其图象是连续不断的,如果存在非零常数
,其图象是连续不断的,如果存在非零常数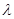 (
(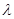 ∈R,使得对任意的x
∈R,使得对任意的x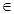 R,都有f(x+
R,都有f(x+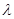 )=
)=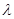 f(x),则称y=f(x)为“倍增函数”,
f(x),则称y=f(x)为“倍增函数”,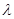 为“倍增系数”,下列命题为真命题的是____(写出所有真命题对应的序号).
为“倍增系数”,下列命题为真命题的是____(写出所有真命题对应的序号).①若函数
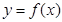 是倍增系数
是倍增系数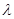 =-2的倍增函数,则
=-2的倍增函数,则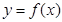 至少有1个零点;
至少有1个零点;②函数
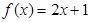 是倍增函数,且倍增系数
是倍增函数,且倍增系数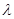 =1;
=1;③函数
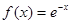 是倍增函数,且倍增系数
是倍增函数,且倍增系数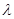 ∈(0,1);
∈(0,1);④若函数
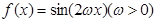 是倍增函数,则
是倍增函数,则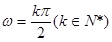
①③④
∵函数y=f(x)是倍增系数λ=-2的倍增函数,∴f(x-2)=-2f(x),
当x=0时,f(-2)+2f(0)=0,若f(0),f(-2)任一个为0,函数f(x)有零点.
若f(0),f(-2)均不为零,则f(0),f(-2)异号,
由零点存在定理,在(-2,0)区间存在x0,f(x0)=0,即y=f(x)至少有1个零点,故①正确;
∵f(x)=2x+1是倍增函数,∴2(x+λ)+1=λ(2x+1),∴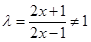 ,故②不正确;
,故②不正确;
∵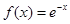 是倍增函数,∴
是倍增函数,∴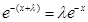 ,∴
,∴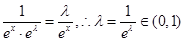 ,故③正确;
,故③正确;
∵f(x)=sin(2ωx)(ω>0)是倍增函数,∴sin[2ω(x+λ)]=λsin(2ωx),
∴ .故④正确.故答案为:①③④.
.故④正确.故答案为:①③④.
当x=0时,f(-2)+2f(0)=0,若f(0),f(-2)任一个为0,函数f(x)有零点.
若f(0),f(-2)均不为零,则f(0),f(-2)异号,
由零点存在定理,在(-2,0)区间存在x0,f(x0)=0,即y=f(x)至少有1个零点,故①正确;
∵f(x)=2x+1是倍增函数,∴2(x+λ)+1=λ(2x+1),∴
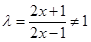 ,故②不正确;
,故②不正确;∵
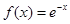 是倍增函数,∴
是倍增函数,∴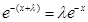 ,∴
,∴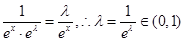 ,故③正确;
,故③正确;∵f(x)=sin(2ωx)(ω>0)是倍增函数,∴sin[2ω(x+λ)]=λsin(2ωx),
∴
 .故④正确.故答案为:①③④.
.故④正确.故答案为:①③④.
练习册系列答案
相关题目
 为同一函数的是( ).
为同一函数的是( ).



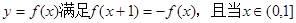 时单调递增,
时单调递增,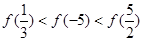
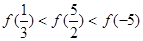
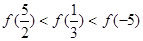
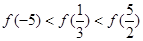
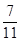
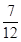
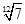 -1
-1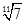 -1
-1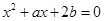 的两根为
的两根为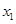 、
、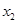 ,且
,且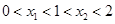 则
则 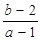 的取值范围是( )
的取值范围是( )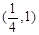
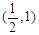
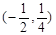

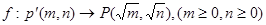 ,现有点
,现有点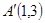 与点
与点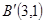 ,点
,点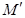 是线段
是线段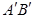 上一动点,按定义的对应法则
上一动点,按定义的对应法则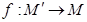 .当点
.当点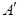 开始运动到点
开始运动到点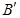 结束时,点
结束时,点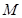 所经过的路线长度为 .
所经过的路线长度为 .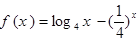 ,
,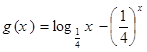 的零点分别为
的零点分别为 ,则( )
,则( )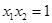
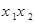 <1
<1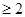
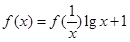 ,则
,则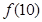 的值为( )
的值为( )