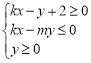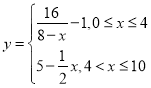题目内容
【题目】已知![]() ,点
,点![]() 是圆
是圆![]() 上的点,
上的点,![]() 是线段
是线段![]() 的中点.
的中点.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 和轨迹
和轨迹![]() 有两个交点
有两个交点![]() (
(![]() 不重合),若
不重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]()
【解析】
试题分析:(Ⅰ)设M(x,y),则P(-5,0)关于M的对称点为Q(2x+5,2y),由此能求出轨迹C的方程.
(Ⅱ)设A![]() ,B
,B![]() ,设直线l的方程是y=k(x+5),由方程组
,设直线l的方程是y=k(x+5),由方程组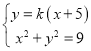 ,得
,得![]() ,由此利用根的判别式和韦达定理能求出直线l的方程.
,由此利用根的判别式和韦达定理能求出直线l的方程.
试题解析:(Ⅰ)设![]() ,则
,则![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
∵点![]() 是圆
是圆![]() 上的点,
上的点,
∴![]() ,即
,即![]() ,
,
所以轨迹![]() 的方程是
的方程是![]() .
.
(Ⅱ)① 设![]() ,由题意,直线
,由题意,直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,则直线
,则直线![]() 的方程是
的方程是![]() ,
,
由方程组![]() 得,
得,![]() ,
,
由![]() ,得
,得![]()
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得,![]() ,∴直线
,∴直线![]() 的方程是
的方程是![]() ,
,
即直线![]() 的方程是
的方程是![]() 或
或![]() .
.
【另解】设坐标原点为![]() ,作
,作![]() ,垂足为
,垂足为![]() .
.
∵![]() ,∴
,∴![]() ,由(I)可知,
,由(I)可知,![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,
,
∴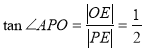 .∴直线
.∴直线![]() 的斜率
的斜率![]() ,∴直线
,∴直线![]() 的方程是
的方程是![]() ,
,
即直线![]() 的方程是
的方程是![]() 或
或![]() .
.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
(1)从该单位中任取2人,此2人中年薪收入高于5万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(2)已知员工年薪收入![]() 与工作所限
与工作所限![]() 成正相关关系,某员工工作第一年至第四年的年薪如下表:
成正相关关系,某员工工作第一年至第四年的年薪如下表:
工作年限 | 1 | 2 | 3 | 4 |
年薪(万元) | 3.0 | 4.2 | 5.6 | 7.2 |
预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式和参考数据分别为:
中系数计算公式和参考数据分别为:
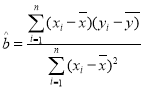 ,
,![]() ,其中
,其中![]() 为样本均值,
为样本均值,![]() ,
,![]() ,(
,(![]() )
)