题目内容
【题目】已知抛物线![]() (
(![]() ),其准线方程为
),其准线方程为![]() ,直线
,直线![]() 过点
过点![]() (
(![]() )且与抛物线交于
)且与抛物线交于![]() 两点,
两点, ![]() 为坐标原点.
为坐标原点.
(1)求抛物线方程,并证明:![]() 的值与直线
的值与直线![]() 倾斜角的大小无关;
倾斜角的大小无关;
(2)若![]() 为抛物线上的动点,记
为抛物线上的动点,记![]() 的最小值为函数
的最小值为函数![]() ,求
,求![]() 的解析式.
的解析式.
【答案】(1)见解析(2)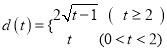
【解析】试题分析:由准线方程可求出抛物线方程![]() ,分直线斜率不存在和存在分类讨论,当斜率存在时,设直线方程
,分直线斜率不存在和存在分类讨论,当斜率存在时,设直线方程![]() 与抛物线组方程组,再利用韦达定理可理。第二问,
与抛物线组方程组,再利用韦达定理可理。第二问, ![]() ,则
,则![]() ,
, ![]() ,,根号内转化为二次函数的三点一轴求最值问题。
,,根号内转化为二次函数的三点一轴求最值问题。
试题解析:(1)方法一:由题意, ![]() ,所以抛物线的方程为
,所以抛物线的方程为![]() .
.
当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,则
,则![]() ,
, ![]() ,
,![]() .
.
当直线![]() 的斜率
的斜率![]() 存在时,则
存在时,则![]() ,设
,设![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,由
,由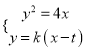 消去
消去![]() ,得
,得![]() ,故
,故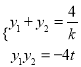 ,所以,
,所以,![]() .
.
综上,![]() 的值与直线
的值与直线![]() 倾斜角的大小无关.
倾斜角的大小无关.
方法二:由题意,![]() ,所以抛物线的方程为
,所以抛物线的方程为![]() .
.
依题意,可设直线![]() 的方程为
的方程为![]() (
(![]() ),
),![]() ,
, ![]() ,由
,由![]() 得
得![]() ,故
,故![]() ,
,
所以, ![]()
![]()
综上,![]() 的值与直线
的值与直线![]() 倾斜角的大小无关.
倾斜角的大小无关.
(2)设![]() ,则
,则![]() ,
, ![]() ,注意到
,注意到![]() ,所以,
,所以,
若![]() ,即
,即![]() ,则当
,则当![]() 时,
时, ![]() 取得最小值,即
取得最小值,即![]() ;
;
若![]() ,即有
,即有![]() ,则当
,则当![]() 时,
时, ![]() 取得最小值,即
取得最小值,即![]() ;
;
综上所述, 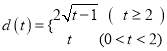

练习册系列答案
相关题目
【题目】甲、乙两名射手在一次射击中的得分是两个随机变量,分别记为X和Y,它们的分布列分别为
X | 0 | 1 | 2 |
P | 0.1 | a | 0.4 |
Y | 0 | 1 | 2 |
P | 0.2 | 0.2 | b |
(1)求a,b的值;
(2)计算X和Y的期望与方差,并以此分析甲、乙两射手的技术情况.