题目内容
17.已知等差数列{an}.(1)若a1+a5+a9=6,求a5.
(2)若a7+a8+a22+a23=28,a7a23=40,求公差d.
分析 (1)直接由已知a1+a5+a9=6,结合等差数列的性质求解答案;
(2)由等差数列的性质可得a7+a23=14,又a7a23=40,结合韦达定理可得a7,a23是方程x2-14x+40=0的根,即可求公差d.
解答 解:(1)∵数列{an}是等差数列,
∴a1+a9=2a5,
∵a1+a5+a9=6,
∴3a5=6,
∴a5=2;
(2)由等差数列的性质可得:a7+a8+a22+a23=2(a7+a23)=28,
故可得a7+a23=14,
又a7a23=40,结合韦达定理可得a7,a23是方程x2-14x+40=0的根,
解之可得x=4或10,
故a7=4,a23=10 或a7=10,a23=4,
故公差d=±$\frac{3}{8}$.
点评 本题考查了等差数列的性质,在等差数列中,若m+n=p+q=2k,且m,n,p,q,k∈N*,则am+an=ap+aq=2ak,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.如图,△ABC中,D,E分别为AB,AC的中点,CD与BE交于F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=m$\overrightarrow{a}$+n$\overrightarrow{b}$,则m+n=( )
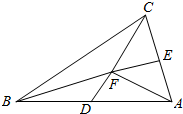

| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
12.在△ABC中,sin2$\frac{A}{2}$=$\frac{c-b}{2c}$(a,b,c分别为角A,B,C的对边),则C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
2.1<|x|<2的解集是( )
| A. | -2<x<2 | B. | x<-1或x>1 | C. | -2<x<-1或1<x<2 | D. | -1<x<-2且1<x<2 |
9.已知0<a<1,方程(x-a)(x-$\frac{1}{a}$)=0的解是( )
| A. | -a,a | B. | a,$\frac{1}{a}$ | C. | -a,$\frac{1}{a}$ | D. | -$\frac{1}{a}$,a |