Question

已知函数f(x)=3sin(

1

2

x-

π

4

)， x∈R．
（1）画出函数f（x）在长度为一个周期的闭区间上的简图；
（2）将函数y=sinx的图象作怎样的变换可得到f（x）的图象？
（3）设函数g（x）=|f（x）|，求g（x）的周期、单调递减区间．

Answer 1

分析：（1）用五点法作函数f（x）在长度为一个周期的闭区间上的简图．
（2）方法一：先把y=sinx的图象向右平移

π

4

个单位，然后把所有点的横坐标扩大为原来的2倍，再把所有点的纵坐标扩大为原来的3倍，得到f（x）的图象．
方法二：先把y=sinx的图象所有点的纵坐标扩大为原来的3倍，然后把所有点的横坐标扩大为原来的2倍，再把图象向右平移

π

2

个单位，得到f（x）的图象．
（3）由题意知，g（x）的周期是函数f（x）的周期的一半，解不等式 

π

2

+kπ≤

1

2

x-

π

4

≤π+kπ， k∈Z，
求得x的范围，即可得到g（x）的单调递减区间．

解答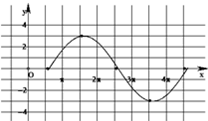：解：（1）函数f（x）的周期T=

2π

1 2

=4π，
由

1

2

x-

π

4

=0，

π

2

，π，

3π

2

，2π，解得x=

π

2

，

3π

2

，

5π

2

，

7π

2

，

9π

2

．列表如下：

x	π 2	3π 2	5π 2	7π 2	9π 2
1 2 x- π 4	0	π 2	π	3π 2	2π
3sin（ 1 2 x- π 4 ）	0	3	0	-3	0

…（3分）
描出五个关键点并光滑连线，得到一个周期的简图．图象如图所示． …（4分）
（2）方法一：先把y=sinx的图象向右平移

π

4

个单位，然后把所有点的横坐标扩大为原来的2倍，再把所有点的纵坐标扩大为原来的3倍，得到f（x）的图象．…（8分）
方法二：先把y=sinx的图象所有点的纵坐标扩大为原来的3倍，然后把所有点的横坐标扩大为原来的2倍，再把图象向右平移

π

2

个单位，得到f（x）的图象．…（8分）
（3）g（x）的周期为T′=T×

1

2

=4π×

1

2

=2π…（9分）
解不等式 

π

2

+kπ≤

1

2

x-

π

4

≤π+kπ， k∈Z，…（10分） 得 

3π

2

+2kπ≤x≤

5π

2

+2kπ， k∈Z，
所以，函数g（x）的单调递减区间为[

3π

2

+2kπ，

5π

2

+2kπ]， k∈Z．…（12分）

点评：本题考查用五点法作y=Asin（ωx+∅）的图象和性质，以及函数y=Asin（ωx+∅）的图象变换，是一道中档题．